【题目】你会求![]() 的值吗?这个问题看上去很复杂,我们可以先考虑简单的情况,通过计算,探索规律:
的值吗?这个问题看上去很复杂,我们可以先考虑简单的情况,通过计算,探索规律:
![]()
![]()
![]()
(1)由上面的规律我们可以大胆猜想,得到![]() =________
=________
利用上面的结论,求
(2)![]() 的值;
的值;
(3)求![]() 的值.
的值.
参考答案:
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]()
【解析】分析:(1)根据已知算式得出规律,即可得出答案;
(2)先变形,再根据规律得出答案即可;
(3)先变形,再根据算式得出即可.
详解:(1)(a﹣1)(a2018+a2017+a2016+…+a2+a+1) =a2019﹣1.
故答案为:a2019﹣1;
(2)22018+22017+22016+…+22+2+1
=(2﹣1)×(22018+22017+22016+…+22+2+1)
=22019﹣1
故答案为:22019﹣1;
(3)∵![]()
∴![]()
∴![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x,y的方程组
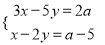 ,则下列结论中正确的是( )
,则下列结论中正确的是( )①当a=5时,方程组的解是
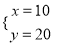 ;
;
②当x,y的值互为相反数时,a=20;③不存在一个实数a使得x=y;
④若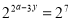 ,则a=2.
,则a=2.A. ①②③④ B. ②③ C. ②③④ D. ②③④
-
科目: 来源: 题型:
查看答案和解析>>【题目】观察下列等式:
12×231=132×21,
13×341=143×31,
23×352=253×32,
34×473=374×43,
62×286=682×26,
……
以上每个等式中两边数字是分别对称的,且每个等式中组成两位数与三位数的数字之间具有相同规律,我们称这类等式为“数字对称等式”.
(1)根据上述各式反映的规律填空,使式子成为“数字对称等式”:
①52× = ×25;
② ×396=693× .
(2)设这类等式左边两位数的十位数字为
 ,个位数字为
,个位数字为 ,且2≤
,且2≤ ≤9,写出表示“数字对称等式”一般规律的式子(含
≤9,写出表示“数字对称等式”一般规律的式子(含 、
、 ),并说明理由.
),并说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】为了打造区域中心城市,实现攀枝花跨越式发展,我市花城新区建设正按投资计划有序推进.花城新区建设工程部,因道路建设需要开挖土石方,计划每小时挖掘土石方540m3,现决定向某大型机械租赁公司租用甲、乙两种型号的挖掘机来完成这项工作,租赁公司提供的挖掘机有关信息如表:

(1)若租用甲、乙两种型号的挖掘机共8台,恰好完成每小时的挖掘量,则甲、乙两种型号的挖掘机各需多少台?
(2)请你设计一种方案,不仅每小时支付的租金最少,又恰好能完成每小时的挖掘量?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,∠BAC=60°,∠ABC、∠ACB的平分线交于E,D是AE延长线上一点,且∠BDC=120°.下列结论:①∠BEC=120°;②DB=DC;③DB=DE;④∠BDE=∠BCA.其中正确结论的个数为( )
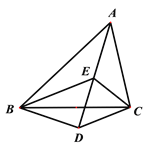
A. 1 B. 2 C. 3 D. 4
-
科目: 来源: 题型:
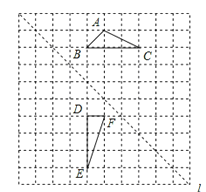
查看答案和解析>>【题目】如图,在边长为1个单位长度的小正方形组成的网格中,给出了格点△ABC和△DEF(顶点为网格线的交点),以及过格点的直线l.
①将△ABC向右平移两个单位长度,再向下平移两个单位长度,画出平移后的三角形△A’B’C’;
②画出△DEF关于直线l对称的三角形△D’E’F’;
③填空:∠C+∠E= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x,y的方程组
 的解满足x<0,y>0.
的解满足x<0,y>0.(1)x=________, y=________(用含a的代数式表示);
(2)求a的取值范围;
(3)若2x8y=2m,用含有a的代数式表示m,并求m的取值范围.
相关试题

