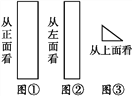
【题目】如图,是某几何体从三个方向分别看到的图形.
(1)说出这个几何体的名称;
(2)画出它的一种表面展开图;
(3)若图①的长为15 cm,宽为4 cm;图②的宽为3 cm;图③直角三角形的斜边长为5 cm,试求这个几何体的所有棱长的和是多少?它的侧面积多大?
参考答案:
【答案】(1)三棱柱(2)如下图所示(3) 69cm;180cm2
【解析】试题分析:(1)根据三视图的形状直接判断即可;
(2)根据(1)的结论,画出侧面展开图即可;
(3)根据题意和侧面展开图,可知侧面棱长(宽×2)为4+3+5=12cm,长为15cm(共3条),然后可求棱长和;再根据长方形的面积公式分别求解,再求和即可.
试题解析:(1)三棱柱;
(2)如下图所示;

(3)棱长和为(3+4+5)×2+15×3=69(cm);
侧面积为3×15+4×15+5×15=180(cm2)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是一个长方体的表面展开图,每个外表面都标注了字母,请根据要求回答问题:
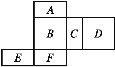
(1)如果面A在多面体的底部,那么哪一个面会在上面?
(2)如果面F在前面,从左面看是面B,那么哪一个面会在上面?
(3)如果从右面看是面C,面D在后面,那么哪一个面会在上面?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,有两种形状不同的直角三角形纸片各两块,其中一种纸片的两条直角边长分别为1和2,另一种纸片的两条直角边长都为2.

图1、图2、图3是三张形状、大小完全相同的方格纸,方格纸中的每个小正方形的边长均为1. 请用三种方法将图中所给四块直角三角形纸片全部用上,互不重叠且不留空隙,三种方法所拼得的平行四边形(非矩形)的周长互不相等,并把你所拼得的图形按实际大小画在图1、图2、图3的方格纸上.
要求:(1)所画图形各顶点必须与方格纸中的小正方形顶点重合;



(2)画图时,要保留四块直角三角形纸片的拼接痕迹.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下列材料:
小明遇到一个问题:AD是△ABC的中线, 点M为BC边上任意一点(不与点D重合),过点M作一直线,使其等分△ABC的面积.
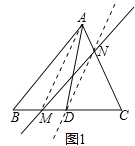
他的做法是:如图1,连结AM,过点D作DN//AM交AC于点N,作直线MN,直线MN即为所求直线.
请你参考小明的做法,解决下列问题:
(1)如图2, AE等分四边形ABCD的面积,M为CD边上一点,过M作一直线MN,使其等分四边形ABCD的面积(要求:在图2中画出直线MN,并保留作图痕迹);
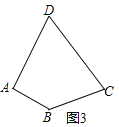
(2)如图3,求作过点A的直线AE,使其等分四边形ABCD的面积(要求:在图3中画出直线AE,并保留作图痕迹).

-
科目: 来源: 题型:
查看答案和解析>>【题目】一堂公开课,老师在黑板上写了两个代数式
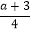 与
与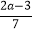 ,让大家相互之间用这两个代数式出题考对方.
,让大家相互之间用这两个代数式出题考对方.(1)小明给小红出的题为:若代数式
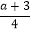 与
与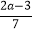 的值多1,求3a2﹣2(2a2+a)+2(a2﹣3a)的值;
的值多1,求3a2﹣2(2a2+a)+2(a2﹣3a)的值;(2)小红想为难一下小明,她给小明出的题为:已知a为负数,比较代数式
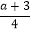 与
与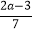 的大小,请你帮小明作出解答.
的大小,请你帮小明作出解答. -
科目: 来源: 题型:
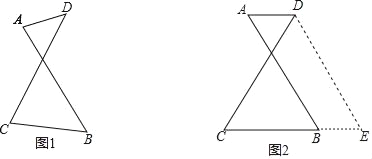
查看答案和解析>>【题目】如图1有两条长度相等的相交线段AB、CD,它们相交的锐角中有一个角为60°,为了探究AD、CB与CD(或AB)之间的关系,小亮进行了如下尝试:
(1)在其他条件不变的情况下使得AD∥BC,如图2,将线段AB沿AD方向平移AD的长度,得到线段DE,然后联结BE,进而利用所学知识得到AD、CB与CD(或AB)之间的关系: ;(直接写出结果)
(2)根据小亮的经验,请对图1的情况(AD与CB不平行)进行尝试,写出AD、CB与CD(或AB)之间的关系,并进行证明;
(3)综合(1)、(2)的证明结果,请写出完整的结论: .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图甲,四边形OABC的边OA、OC分别在x轴、y轴的正半轴上,顶点在B点的抛物线交x轴于点A、D,交y轴于点E,连接AB、AE、BE.已知tan∠CBE=
 ,A(3,0),D(﹣1,0),E(0,3).
,A(3,0),D(﹣1,0),E(0,3).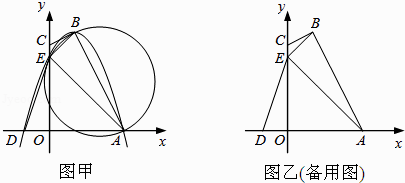
(1)求抛物线的解析式及顶点B的坐标;
(2)求证:CB是△ABE外接圆的切线;
(3)试探究坐标轴上是否存在一点P,使以D、E、P为顶点的三角形与△ABE相似,若存在,直接写出点P的坐标;若不存在,请说明理由;
(4)设△AOE沿x轴正方向平移t个单位长度(0<t≤3)时,△AOE与△ABE重叠部分的面积为s,求s与t之间的函数关系式,并指出t的取值范围.
相关试题

