搜索
【题目】如图是一个长方体的表面展开图,每个外表面都标注了字母,请根据要求回答问题:
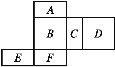
(1)如果面A在多面体的底部,那么哪一个面会在上面?
(2)如果面F在前面,从左面看是面B,那么哪一个面会在上面?
(3)如果从右面看是面C,面D在后面,那么哪一个面会在上面?
参考答案：
【答案】(1)面F.(2)面C.(3)面A.
【解析】
利用长方体及其表面展开图的特点解题．这是一个正方体的平面展开图，共有六个面，其中面“A”与面“F”相对，面“B”与面“D”相对，“C”与面“E”相对．
由图可知，“C”与面“E”相对．则
（1）∵面“A”与面“F”相对，∴A面是长方体的底部时，F面在上面；
（2）由图可知，如果F面在前面，B面在左面，那么“E”面在下面，∵面“C”与面“E”相对， ∴C面会在上面；
（3）由图可知，如果C面在右面，D面在后面，那么“F”面在下面，∵面“A”与面“F”相对，∴A面在上面．
A面会在上面．
-
科目： 来源： 题型：
查看答案和解析>>【题目】同学们都知道，|5﹣（﹣2）|表示5与﹣2之差的绝对值，实际上也可理解为5与﹣2两数在数轴上所对的两点之间的距离．试探索：
（1）求|5﹣（﹣2）|=________．
（2）数轴上表示x和﹣1的两点之间的距离表示为________．
（3）找出所有符合条件的整数x，使|x+5|+|x﹣2|=7，这样的整数有________个．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图①是一个长为2m，宽为2n的长方形（m＞n），沿图中虚线用剪刀均匀分民四块小长方形，然后按图②的形状拼成一个正方形．
（1）图②中阴影部分的正方形的边长是多少？（用代数式表示）
（2）观察图②写出下列三个代数式：（m+n）2 ， （m﹣n）2 ， mn之间的等量关系．
（3）若m+n=7，mn=6，求m-n．
-
科目： 来源： 题型：
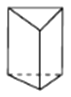
查看答案和解析>>【题目】观察下列多面体，并把下表补充完整.
名称
三棱柱
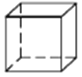
四棱柱
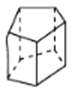
五棱柱
六棱柱
图形
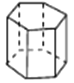
顶点数
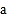
6
10
12
棱数
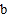
9
12
面数
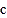
5
8
观察上表中的结果，你能发现
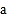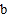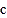、、之间有什么关系吗？请写出关系式. -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，有两种形状不同的直角三角形纸片各两块，其中一种纸片的两条直角边长分别为1和2，另一种纸片的两条直角边长都为2.
图1、图2、图3是三张形状、大小完全相同的方格纸，方格纸中的每个小正方形的边长均为1. 请用三种方法将图中所给四块直角三角形纸片全部用上，互不重叠且不留空隙，三种方法所拼得的平行四边形（非矩形）的周长互不相等，并把你所拼得的图形按实际大小画在图1、图2、图3的方格纸上.
要求：（1）所画图形各顶点必须与方格纸中的小正方形顶点重合；
（2）画图时，要保留四块直角三角形纸片的拼接痕迹.
-
科目： 来源： 题型：
查看答案和解析>>【题目】阅读下列材料：
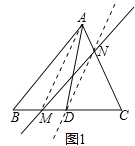
小明遇到一个问题：AD是△ABC的中线， 点M为BC边上任意一点（不与点D重合），过点M作一直线，使其等分△ABC的面积．
他的做法是：如图1，连结AM，过点D作DN//AM交AC于点N，作直线MN，直线MN即为所求直线．
请你参考小明的做法，解决下列问题：
（1）如图2， AE等分四边形ABCD的面积，M为CD边上一点，过M作一直线MN，使其等分四边形ABCD的面积（要求：在图2中画出直线MN，并保留作图痕迹）；
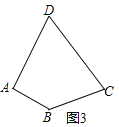
（2）如图3，求作过点A的直线AE，使其等分四边形ABCD的面积（要求：在图3中画出直线AE，并保留作图痕迹）．
-
科目： 来源： 题型：
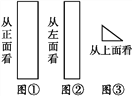
查看答案和解析>>【题目】如图,是某几何体从三个方向分别看到的图形.
(1)说出这个几何体的名称;
(2)画出它的一种表面展开图;
(3)若图①的长为15 cm,宽为4 cm;图②的宽为3 cm;图③直角三角形的斜边长为5 cm,试求这个几何体的所有棱长的和是多少?它的侧面积多大?
相关试题
