【题目】阅读下面材料:
在学习《圆》这一章时,老师给同学们布置了一道尺规作图题:
尺规作图:过圆外一点作圆的切线。
已知:P为⊙O外一点。
求作:经过点P的⊙O的切线
小敏的作法如下:
如图:
①连接OP,作线段OP的垂直平分线MN交OP于C
②以点C为圆心,CO的长为半径作圆,交⊙O 于A,B两点
③作直线PA,PB所以直线PA,PB就是所求的切线
老师认为小敏的作法正确.
请回答:连接OA,OB后,可证∠OAP=∠OBP=90°,其依据是;由此可证明直线PA,PB都是⊙O的切线,其依据是 .
参考答案:
【答案】直径所对的圆周角是直角;经过半径外端并且垂直于这条半径的直线是圆的切线
【解析】解:∵OP是⊙O的直径,
∴∠OAP=∠OBP=90°.
∴直线PA,PB都是⊙O的切线.
所以答案是:直径所对的圆周角是直角;经过半径外端并且垂直于这条半径的直线是圆的切线.
-
科目: 来源: 题型:
查看答案和解析>>【题目】“幸福是奋斗出来的”,在数轴上,若C到A的距离刚好是3,则C点叫做A的“幸福点”,若C到A、B的距离之和为6,则C叫做A、B的“幸福中心”
(1)如图1,点A表示的数为﹣1,则A的幸福点C所表示的数应该是 ;
(2)如图2,M、N为数轴上两点,点M所表示的数为4,点N所表示的数为﹣2,点C就是M、N的幸福中心,则C所表示的数可以是 (填一个即可);
(3)如图3,A、B、P为数轴上三点,点A所表示的数为﹣1,点B所表示的数为4,点P所表示的数为8,现有一只电子蚂蚁从点P出发,以2个单位每秒的速度向左运动,当经过多少秒时,电子蚂蚁是A和B的幸福中心?

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知A=3a2b﹣2ab2+abc,小明同学错将“2A﹣B“看成”2A+B“,算得结果为4a2b﹣3ab2+4abc.
(1)计算B的表达式;
(2)求出2A﹣B的结果;
(3)小强同学说(2)中的结果的大小与c的取值无关,对吗?若a=
 ,b=
,b= ,
,求(2)中式子的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】我市某中学举办“网络安全知识答题竞赛”,初、高中部根据初赛成绩各选出5名选手组成初中代表队和高中代表队参加学校决赛,两个队各选出的5名选手的决赛成绩如图所示.
平均分(分)
中位数(分)
众数(分)
方差(分2)
初中部
a
85
b
s初中2
高中部
85
c
100
160
(1)根据图示计算出a、b、c的值;
(2)结合两队成绩的平均数和中位数进行分析,哪个队的决赛成绩较好?
(3)计算初中代表队决赛成绩的方差s初中2,并判断哪一个代表队选手成绩较为稳定.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数的解析式是y=x2﹣2x﹣3.
(1)与x轴的交点坐标是;顶点坐标是;
(2)在坐标系中利用描点法画出此抛物线.x
…
…
y
…
…

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示的是一个长
 ,宽
,宽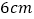 ,高
,高 的长方体,现在把它等分为
的长方体,现在把它等分为 个棱长为
个棱长为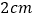 的小正方体
的小正方体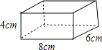
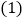 说明你的分法;
说明你的分法; 把这
把这 个小正方体排成一排组成一个新长方体,这个新长方体与原长方体相比.表面积怎样变化?
个小正方体排成一排组成一个新长方体,这个新长方体与原长方体相比.表面积怎样变化? -
科目: 来源: 题型:
查看答案和解析>>【题目】某工厂车间共有10名工人,调查每个工人的日均生产能力,获得数据制成如下统计图.
(1)求这10名工人的日均生产件数的平均数、众数、中位数;
(2)若要使占60%的工人都能完成任务,应选什么统计量(平均数、中位数、众数)做日生产件数的定额?

相关试题

