【题目】如图,直线![]() 与坐标轴分别交于点
与坐标轴分别交于点![]() ,与直线
,与直线![]() 交于点
交于点![]() 是线段
是线段![]() 上的动点,连接
上的动点,连接![]() ,若
,若![]() 是等腰三角形,则
是等腰三角形,则![]() 的长为___________.
的长为___________.

参考答案:
【答案】2或![]() 或4
或4
【解析】
先求出直线![]() 与直线
与直线![]() 交点C的坐标,若使
交点C的坐标,若使![]() 是等腰三角形,分三种情况讨论,即OQ=CQ或OC=OQ或OC=CQ,在直角三角形中利用勾股定理,根据等腰三角形的性质即可求出OQ.
是等腰三角形,分三种情况讨论,即OQ=CQ或OC=OQ或OC=CQ,在直角三角形中利用勾股定理,根据等腰三角形的性质即可求出OQ.
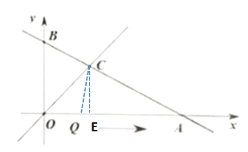
①如图,当OQ=CQ时,过点C作CE⊥OA于点E,
直线![]() 与直线
与直线![]() 交于点C,
交于点C,
![]()
得x=2,
y=x=2
∴C(2,2)
设OQ=CQ=x,QE=2-x
在Rt△CEQ中![]()
解得x=2
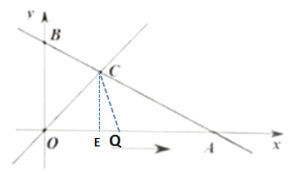
②当OC=OQ时,过点C作CE⊥OA于点E,C(2,2)
在Rt△CEO中, ![]()
OC=![]()
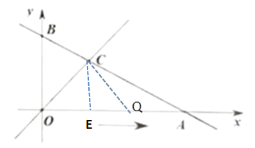
③当OC=CQ时, 过点C作CE⊥OA于点E
∵OC=CQ
∴OE=EQ=2
∴OQ=2OE=4
综上所示,若![]() 是等腰三角形,OQ的长为2或
是等腰三角形,OQ的长为2或![]() 或4
或4
故答案为:2或![]() 或4
或4
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个机器人从数轴原点出发,沿数轴正方向,以每前进3步后退2步的程序运动;设该机器人每秒钟前进或后退1步,并且每步的距离是1个单位长,xn表示第n秒时机器人在数轴上的位置所对应的数;给出下列结论:(1)x3=3;(2)x5=1;(3)x108<x104;其中,正确结论的序号是( )
A. (1)、(3)B. (2)、(3)C. (1)、(2)D. (1)、(2)、(3)
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1)7(4)+(5);
(2)
 ;
; (3)
 ;
; (4)(
 +
+  -
-  )×(-12);
)×(-12); (5)
 ;
; (6)
 ;
; -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,是由7块颜色不同的正方形组成的长方形,已知中间小正方形的边长为1,这个长方形的面积为( )

A.45B.48C.63D.64
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)观察下列图形与等式的关系,并填空:
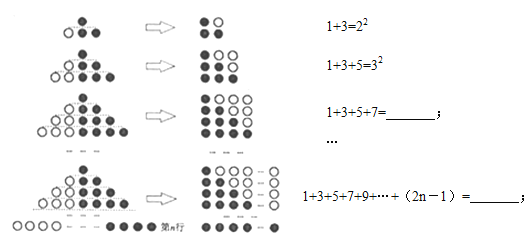
(2)利用(1)中结论,解决下列问题:
①1+3+5+…+2005= ;
②计算:101+103+105+…+199;
-
科目: 来源: 题型:
查看答案和解析>>【题目】若A、B、C为数轴上三点,若点C到A的距离是点C到B的距离2倍,我们就称点C是(A,B)的好点.例如,如图1,点A表示的数为﹣1,点B表示的数为2.表示1的点C到点A的距离是2,到点B的距离是1,那么点C是(A,B)的好点;又如,表示0的点D到点A的距离是1,到点B的距离是2,那么点D就不是(A,B)的好点,但点D是(B,A)的好点.

知识运用:如图2,M、N为数轴上两点,点M所表示的数为﹣2,点N所表示的数为4.

(1)数 所表示的点是(M,N)的好点;
(2)如图3,A、B为数轴上两点,点A所表示的数为﹣20,点B所表示的数为40.现有一只电子蚂蚁P从点B出发,以2个单位每秒的速度向左运动,到达点A停止.当t为何值时,P、A和B中恰有一个点为其余两点的好点?

-
科目: 来源: 题型:
查看答案和解析>>【题目】用无刻度直尺作图并解答问题:
如图,
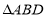 和
和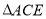 都是等边三角形,在
都是等边三角形,在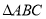 内部做一点
内部做一点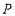 ,使得
,使得 ,并给予证明.
,并给予证明.
相关试题

