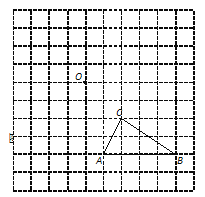
【题目】在如图的正方形网格中,每个小正方形的边长都是单位1,△ABC的顶点均在格点上.
(1)画出△ABC向左平移2个单位,然后再向上平移4个单位后的△A1B1C1;
(2)画出△A2B2C2,使△A2B2C2和△A1B1C1关于点O成中心对称;
(3)指出如何平移△ABC,使得△A2B2C2和△ABC能拼成一个平行四边形.
参考答案:
【答案】(1)画图见解析;(2)画图见解析;(3)答案不唯一,具体见解析.
【解析】试题分析:(1)将A、B、C分别向左平移2个单位,然后再向上平移4个单位,顺次连接即可得出△A1B1C1;
(2)根据中心对称的性质,找到各点的对应点,顺次连接可得出△A2B2C2;
(3)平移△ABC,使得△A2B2C2和△ABC的三边中的一边重合即可.
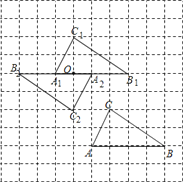
试题解析:(1)如图所示:△A1B1C1即为所求;
(2)如图所示:△A2B2C2即为所求;
(3)答案不唯一.
如:①先将△ABC向左平移1个单位,然后再向上平移2个单位.
②先将△ABC向左平移4个单位,然后再向上平移4个单位.
③先将△ABC向左平移5个单位,然后再向上平移2个单位.
-
科目: 来源: 题型:
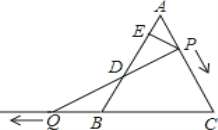
查看答案和解析>>【题目】如图,△ABC是边长为6的等边三角形,P是AC边上一动点,由A向C运动(与A、C不重合),Q是CB延长线上一点,与点P同时以相同的速度由B向CB延长线方向运动(Q不与B重合),过P作PE⊥AB于E,连接PQ交AB于D.
(1)当∠BQD=30°时,求AP的长;
(2)证明:在运动过程中,点D是线段PQ的中点;
(3)当运动过程中线段ED的长是否发生变化?如果不变,求出线段ED的长;如果变化请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算(-xy2)3的结果是( )
A. -x3y6 B. x3y6 C. x4y5 D. -x4y5
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图①,点O为直线AB上一点,过点O作射线OC,使∠AOC=60°.将一把直角三角尺的直角顶点放在点O处,一边OM在射线OB上,另一边ON在直线AB的下方,其中∠OMN=30°.
(1)将图①中的三角尺绕点O顺时针旋转至图②,使一边OM在∠BOC的内部,且恰好平分∠BOC,则∠CON=________;
(2)将图①中的三角尺绕点O按每秒10°的速度沿顺时针方向旋转一周,在旋转的过程中,在第________秒时,边MN恰好与射线OC平行;在第________秒时,直线ON恰好平分锐角∠AOC(直接写出结果);
(3)将图①中的三角尺绕点O顺时针旋转至图③,使ON在∠AOC的内部,请探究∠AOM与∠NOC之间的数量关系,并说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】完成下列推理说明:如图,已知AB∥DE,且有∠1=∠2,∠3=∠4,

∵AB∥DE( )
∴∠1= (根据两直线平行,同位角相等)
∵∠1= , ∠3=∠4(已知)
∴∠2= (等量代换)
∴BC∥EF(根据___________________________)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC.中,AB=BC,将△ABC绕点B顺时针旋转α度,得到△A1BC1,A1B交AC于点E,A1C1分别交AC、BC于点D、F,下列结论:①∠CDF=α,②A1E=CF,③DF=FC,④A1F=CE.其中正确的是 (写出正确结论的序号).

-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)如图所示,选择适当的方向击打白球,可以使白球 反弹后将黑球撞入袋中,此时∠1=∠2,并且∠2 +∠3=90°。如果∠3=30°,那么∠1应等于多少度,才能保证黑球直接入袋?
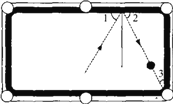
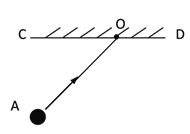
(2)如图,打台球时,小球由A点出发撞击到台球桌边CD的点O处,请用尺规作图的方法作出小球反弹后的运动方向(不写作法,但要保留作图痕迹)
相关试题

