搜索
【题目】已知
.
(1)在如图所示的平面直角坐标系中描出各点，画出
;
(2)将先向左平移3个单位长度，再向下平移5个单位长度，得到
， 请画出
(3)求的面积;
(4)设点
在坐标轴上，且
与的面积相等，请直接写出点的坐标
参考答案：
【答案】（1）详见解析；（2）详见解析；（3）4；（4）点P的坐标
或
【解析】
（1）描点、连线即可完成.
（2）分别作出平移后的对应点，再顺次连接即可得；
（3）利用割补法求解可得；
（4）分两种情况：①当点P在x轴上时；②当点P在y轴上时；根据
的面积，即可求出点P坐标.
解：（1）
为所求；
（2）图中的
为所求；
（3）
（4）当点P在x轴上时，由的面积=4，求得：BP=8，故点P的坐标为（10,0）或（-6,0）；当点P在y轴上时，的面积=4，求得：AP=4.所以点P的坐标为（0,5）或（0，-3）
∴点P的坐标 或
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在平面直角坐标系中，Rt△ABC的三个顶点分别是A(－3，2)，B(0，4)，C(0，2)．
(1)将△ABC以点C为旋转中心旋转180°，画出旋转后对应的△A1B1C；平移△ABC，若点A的对应点A2的坐标为(0，－4)，画出平移后对应的△A2B2C2；
(2)若将△A1B1C绕某一点旋转可以得到△A2B2C2，请直接写出旋转中心的坐标；
(3)在x轴上有一点P，使得PA＋PB的值最小，请直接写出点P的坐标．
-
科目： 来源： 题型：
查看答案和解析>>【题目】一列快车由甲地开往乙地，一列慢车由乙地开往甲地，两车同时出发，匀速运动．快车离乙地的路程
与行驶的时间
之间的函数关系，如图中线段AB所示．慢车离乙地的路程
与行驶的时间之间的函数关系，如图中线段OC所示．根据图象进行以下研究．
快车的速度是________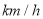
，慢车的速度是________；
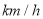求AB与OC的函数关系式．
何时快车离乙地的距离大于慢车离乙地的距离？
-
科目： 来源： 题型：
查看答案和解析>>【题目】甲、乙两家工厂生产的办公桌和办公椅的质量、价格一致， 每张办公桌800元，每把椅子80元，甲、乙两个厂家推出各自销售的优惠方案:甲厂家，买张桌子送三把椅子:乙厂家，桌子和椅子全部按原价的8折优惠现某公司要购买3张办公桌和若干把椅子，若购买的椅子数为x把(
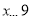) .(1)分别用含x的式子表示购买甲、乙两个厂家桌椅所需的金额:购买甲厂家的桌椅所需金额为_ ；购买乙厂家的桌椅所需金额为_
(2)该公司到哪家工厂购买更划算?
-
科目： 来源： 题型：
查看答案和解析>>【题目】每年的6月5日为世界环保日，为了提倡低碳环保，某公司决定购买10台节省能源的新设备，现有甲、乙两种型号的设备可供选购. 经调查：购买3台甲型设备比购买2台乙型设备多花16万元，购买2台甲型设备比购买3台乙型设备少花6万元.
(1)求甲、乙两种型号设备的价格；
(2)该公司经预算决定购买节省能源的新设备的资金不超过110万元，你认为该公司有哪几种购买方案；
(3)在（2）的条件下，已知甲型设备的产量为240吨/月，乙型设备的产量为180吨/月.若每月要求总产量不低于2040吨，为了节约资金，请你为该公司设计一种最省钱的购买方案.
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，△ABC是等边三角形，BD是中线，延长BC至E，CE=CD，
（1）求证：DB=DE
（2）在图中过D作DF⊥BE交BE于F，若CF=4，求△ABC的周长．
-
科目： 来源： 题型：
查看答案和解析>>【题目】阅读下列材料并解决有关问题：
我们知道，|m|=
．现在我们可以用这一结论来化简含有绝对值的代数式，如化简代数式|m+1|+|m﹣2|时，可令 m+1=0 和 m﹣2=0，分别求得 m=﹣1，m=2（称﹣1，2 分别为|m+1|与|m﹣2|的零点值）．在实数范围内， 零点值 m=﹣1 和 m=2 可将全体实数分成不重复且不遗漏的如下 3 种情况：
（1）m＜﹣1；（2）﹣1≤m＜2；（3）m≥2．从而化简代数式|m+1|+|m﹣2| 可分以下 3 种情况：
（1）当 m＜﹣1 时，原式=﹣（m+1）﹣（m﹣2）=﹣2m+1；
（2）当﹣1≤m＜2 时，原式=m+1﹣（m﹣2）=3；
（3）当 m≥2 时，原式=m+1+m﹣2=2m﹣1．
综上讨论，原式=
通过以上阅读，请你解决以下问题：
（1）分别求出|x﹣5|和|x﹣4|的零点值；
（2）化简代数式|x﹣5|+|x﹣4|；
（3）求代数式|x﹣5|+|x﹣4|的最小值．
相关试题
