【题目】阅读下列材料并解决有关问题：

我们知道，|m|= ．现在我们可以用这一结论来化简含有绝对值的代

数式，如化简代数式|m+1|+|m﹣2|时，可令 m+1=0 和 m﹣2=0，分别求得 m=﹣1，m=2（称﹣1，2 分别为|m+1|与|m﹣2|的零点值）．在实数范围内， 零点值 m=﹣1 和 m=2 可将全体实数分成不重复且不遗漏的如下 3 种情况：

（1）m＜﹣1；（2）﹣1≤m＜2；（3）m≥2．从而化简代数式|m+1|+|m﹣2| 可分以下 3 种情况：

（1）当 m＜﹣1 时，原式=﹣（m+1）﹣（m﹣2）=﹣2m+1；

（2）当﹣1≤m＜2 时，原式=m+1﹣（m﹣2）=3；

（3）当 m≥2 时，原式=m+1+m﹣2=2m﹣1．

综上讨论，原式=

通过以上阅读，请你解决以下问题：

（1）分别求出|x﹣5|和|x﹣4|的零点值；

（2）化简代数式|x﹣5|+|x﹣4|；

（3）求代数式|x﹣5|+|x﹣4|的最小值．

参考答案：

【答案】（1）5 和 4；（2）原式=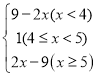；（3）1.

【解析】

试题（1）令 x﹣5=0，x﹣4=0，解得 x 的值即可；（2）分为 x＜4、4≤x＜5、x≥5 三种情况化简即可；（3）根据（2）中的化简结果判断即可．

试题解析：

（1）令 x﹣5=0，x﹣4=0， 解得：x=5 和 x=4， 故|x﹣5|和|x﹣4|的零点值分别为 5 和 4；

（2）当 x＜4 时，原式=5﹣x+4﹣x=9﹣2x； 当 4≤x＜5 时，原式=5﹣x+x﹣4=1；

当 x≥5 时，原式=x﹣5+x﹣4=2x﹣9．

综上讨论，原式=．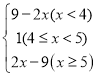

（3）当 x＜4 时，原式=9﹣2x＞1； 当 4≤x＜5 时，原式=1；

当 x≥5 时，原式=2x﹣9＞1．

故代数式的最小值是 1．

关闭