【题目】已知:如图,在![]() 中,
中,![]() ,
,![]() ,垂足为点
,垂足为点![]() ,
,![]() 是
是![]() 外角
外角![]() 的平分线,
的平分线,![]() ,垂足为点
,垂足为点![]() ,连接
,连接![]() 交
交![]() 于点
于点![]() .
.

![]() 求证:四边形
求证:四边形![]() 为矩形;
为矩形;
![]() 当
当![]() 满足什么条件时,四边形
满足什么条件时,四边形![]() 是一个正方形?并给出证明.
是一个正方形?并给出证明.
![]() 在
在![]() 的条件下,若
的条件下,若![]() ,求正方形
,求正方形![]() 周长.
周长.
参考答案:
【答案】![]() 证明见解析;(2)
证明见解析;(2)![]() 且
且![]() 时,四边形
时,四边形![]() 是一个正方形;(3)8.
是一个正方形;(3)8.
【解析】
(1)根据已知条件证明∠DAE=90°,已知CE⊥AN,AD⊥BC,根据有三个角是直角的四边形是矩形,可以证明四边形ADCE为矩形;(2)![]() 且
且![]() 时,四边形
时,四边形![]() 是一个正方形,根据添加的条件证明
是一个正方形,根据添加的条件证明![]() ,即可判定四边形ADCE为正方形;(3)根据勾股定理求得AD的长,根据正方形的性质即可求得正方形ADCE周长.
,即可判定四边形ADCE为正方形;(3)根据勾股定理求得AD的长,根据正方形的性质即可求得正方形ADCE周长.
![]() 证明:∵
证明:∵![]() ,
,![]() ,垂足为点
,垂足为点![]() ,
,
∴![]() .
.
∵![]() 是
是![]() 外角
外角![]() 的平分线,
的平分线,
∴![]() .
.
∵![]() 与
与![]() 是邻补角,
是邻补角,
∴![]() ,
,
∴![]() .
.
即∠DAE=90°,
∵![]() ,
,![]() ,
,
∴![]() ,
,
∴四边形![]() 为矩形;
为矩形;
![]() 且
且![]() 时,四边形
时,四边形![]() 是一个正方形,
是一个正方形,
证明:∵![]() 且
且![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() .
.
∵四边形![]() 为矩形,
为矩形,
∴四边形![]() 为正方形;
为正方形;
![]() 由勾股定理,得
由勾股定理,得
![]() ,
,![]() ,
,
即![]() ,
,
![]() ,
,
正方形![]() 周长
周长![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD中,∠BAD=110°,∠B=∠D=90°,在BC、CD上分别找一点M、N,使△AMN周长最小,此时∠MAN的度数为_________°.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在边长为
 的正方形
的正方形 中,点
中,点 是边
是边 中点,点
中点,点 在边
在边 上,且
上,且 ,设
,设 与
与 交于点
交于点 ,则
,则 的面积是________.
的面积是________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】从边长为a的正方形中剪掉一个边长为b的正方形(如图1),然后将剩余部分拼成一个长方形(如图2).
(1)上述操作能验证的等式是________(填A或B或C)
A.a2-2ab+b2=(a-b)2
B.a2-b2=(a+b)(a-b)
C.a2+ab=a(a+b)
(2)应用你从(1)中选出的等式,完成下列各题:
①已知x2-4y2=12,x+2y=4,求x-2y的值
②计算:(1-
 )(1-
)(1- )(1-
)(1- )…(1-
)…(1- )(1-
)(1- )
)
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)如图矩形
 的对角线
的对角线 、
、 交于点
交于点 ,过点
,过点 作
作 ,且
,且 ,连接
,连接 ,判断四边形
,判断四边形 的形状并说明理由.
的形状并说明理由.(2)如果题目中的矩形变为菱形,结论应变为什么?说明理由.
(3)如果题目中的矩形变为正方形,结论又应变为什么?说明理由.



-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:正方形
 中,点
中,点 、
、 、
、 、
、 分别在
分别在 、
、 、
、 、
、 上,且
上,且 ,
,
 四边形
四边形 是正方形吗?为什么?
是正方形吗?为什么? 若正方形
若正方形 的边长为
的边长为 ,且
,且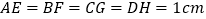 ,请求出四边形
,请求出四边形 的面积.
的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
 中,
中, ,
, ,
, 为
为 的中点,
的中点, 于
于 .
.(1)求
 的度数;
的度数;(2)若
 ,求
,求 的长.
的长.
相关试题

