【题目】2018年9月第22号台风“山竹”给某地造成严重影响.蓝天救援队驾着冲锋舟沿一条东西方向的河流营救灾民,早晨从![]() 地出发,晚上最后到达
地出发,晚上最后到达![]() 地,约定向东为正方向,当天航行依次记录如下(单位:千米):11,-6,15,-7,18,-8,10,-5,问:
地,约定向东为正方向,当天航行依次记录如下(单位:千米):11,-6,15,-7,18,-8,10,-5,问:
(1)![]() 地在
地在![]() 地的东面,还是西面?与
地的东面,还是西面?与![]() 地相距多少千米?
地相距多少千米?
(2)冲锋舟离开出发地最远是多少千米?
(3)若冲锋舟每千米耗油0.5升,油箱容量为30升,求途中至少需要补充多少升油?
参考答案:
【答案】(1)![]() 地在
地在![]() 地的东面,与
地的东面,与![]() 地相距28千米;(2)冲锋舟离开出发地最远是33千米;(3)途中至少需要补充10升油.
地相距28千米;(2)冲锋舟离开出发地最远是33千米;(3)途中至少需要补充10升油.
【解析】
(1)将航行记录的距离相加即可得出答案;
(2)根据航行记录下的数据,依次计算出每次记录时冲锋舟距离出发地的距离,找出其中的最大值即可;
(3)先计算出冲锋舟行驶的总距离,从而可得出总耗油量,再根据油箱容量为30升即可得出答案.
(1)![]()
![]()
![]()
![]()
因![]() ,向东为正方向
,向东为正方向
故![]() 地在
地在![]() 地的东面,与
地的东面,与![]() 地相距28千米;
地相距28千米;
(2)每次记录时,冲锋舟距离出发地的距离依次如下:
第一次为![]()
第二次为![]()
第三次为![]()
第四次为![]()
第五次为![]()
第六次为![]()
第七次为![]()
第八次为![]()
因此,冲锋舟离开出发地最远是33千米;
(3)冲锋舟行驶的总距离为![]()
![]()
![]() (千米)
(千米)
冲锋舟航行中的总耗油量为![]() (升)
(升)
途中至少需要补充的油量为![]() (升)
(升)
故途中至少需要补充10升油.
-
科目: 来源: 题型:
查看答案和解析>>【题目】△ABC中,∠ACB=90°,AC=BC,直线l经过点C,BD⊥l,AE⊥l,,垂足分别为D、E.
(1)当A、B在直线l同侧时,如图1,
①证明:△AEC≌△CDB;
②若AE=3,BD=4,计算△ACB的面积.(提示:间接求)
(2)当A. B在直线l两侧时,如图2,若AE=3,BD=4,连接AD,BE直接写出梯形ADBE的面积___.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,O是直线AB上一点,OC为任意一条射线,OD平分∠BOC,OE平分∠AOC.
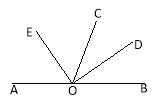
(1)指出图中∠AOD与∠BOE的补角;
(2)试判断∠COD与∠COE具有怎样的数量关系.并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知A、B两地相距4km,上午8:00时,亮亮从A地步行到B地,8:20时芳芳从B地出发骑自行车到A地,亮亮和芳芳两人离A地的距离S(km)与亮亮所用时间t(min)之间的函数关系如图所示,芳芳到达A地时间为( )
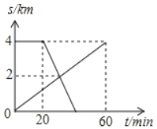
A. 8:30 B. 8:35 C. 8:40 D. 8:45
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC=5,∠B=∠C,BC=8,点D从B点出发沿线段BC向C运动(D不与B、C重合),点E从点C出发沿线段CA向A运动(E不与A、C重合),它们以相同的速度同时运动,连结AD、DE.若要使△ABD≌△DCE,①请给出确定D、E两点位置的方法(如指明CD长度等),并说明理由;②此时∠ADE与∠C大小关系怎样?为什么?

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:O是直线AB上的一点,
 是直角,OE平分
是直角,OE平分 .
.(1)如图1.若
 .求
.求 的度数;
的度数;(2)在图1中,
 ,直接写出
,直接写出 的度数(用含a的代数式表示);
的度数(用含a的代数式表示);(3)将图1中的
 绕顶点O顺时针旋转至图2的位置,探究
绕顶点O顺时针旋转至图2的位置,探究 和
和 的度数之间的关系.写出你的结论,并说明理由.
的度数之间的关系.写出你的结论,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图, BD 是△ABC 的角平分线, AE⊥ BD ,垂足为 F ,若∠ABC=35°,∠ C=50°,则∠CDE 的度数为( )

A.35°B.40°C.45°D.50°
相关试题

