【题目】△ABC中,∠ACB=90°,AC=BC,直线l经过点C,BD⊥l,AE⊥l,,垂足分别为D、E.
(1)当A、B在直线l同侧时,如图1,
①证明:△AEC≌△CDB;
②若AE=3,BD=4,计算△ACB的面积.(提示:间接求)
(2)当A. B在直线l两侧时,如图2,若AE=3,BD=4,连接AD,BE直接写出梯形ADBE的面积___.

参考答案:
【答案】(1)①见解析;②12.5;(2)3.5
【解析】
(1)①根据垂直定义求出∠AEC=∠BDC=90°,求出∠EAC+∠ACE=90°,∠BCD+∠ACE=90°,求出∠EAC=∠BCD,根据AAS推出△AEC≌△CDB;
②根据全等三角形的性质推出CE=BD和AE=CD即可,再利用勾股定理得出AC和BC的长计算即可;
(2)根据垂直定义求出∠AEC=∠BDC=90°,求出∠EAC+∠ACE=90°,∠BCD+∠ACE=90°,求出∠EAC=∠BCD,根据AAS推出△AEC≌△CDB,根据全等三角形的性质推出CE=BD和AE=CD即可,利用梯形面积解答即可.
(1)①∵直线l过点C,BD⊥l,AE⊥l,
∴∠AEC=∠BDC=90°,
∵∠ACB=90°,
∴∠EAC+∠ACE=90°,∠BCD+∠ACE=90°,
∴∠EAC=∠BCD,
在△AEC和△CDB中,
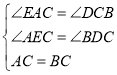 ,
,
∴△AEC≌△CDB(AAS);
②∵△AEC≌△CDB,
∴CE=BD,AE=CD,∠ACE=∠DBC,
∵ED=CE+CD,∠DBC+∠BCD=90°,
∴ED=AE+BD,∠ACE+∠BCD=90°,
在Rt△ACB中,AC=BC=![]() =5,
=5,
∴△ACB的面积=![]() ×5×5=12.5;
×5×5=12.5;
(2)∵直线l过点C,BD⊥l,AE⊥l,
∴∠AEC=∠BDC=90°,
∵∠ACB=90°,
∴∠EAC+∠ACE=90°,∠BCD+∠ACE=90°,
∴∠EAC=∠BCD,
在△AEC和△CDB中,
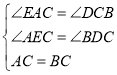 ,
,
∴△AEC≌△CDB(AAS),
∴CE=BD,AE=CD,
∵ED=CECD,
∴ED=BDAE=43=1,
梯形ADBE的面积=![]() ×(3+4)×1=3.5.
×(3+4)×1=3.5.
故答案为:3.5.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)画出△ABC关于直线L的对称图形.

(2)如图,四边形ABCD是矩形,用直尺和圆规作出∠A的平分线与BC边的垂直平分线的交点Q(不写作法,保留作图痕迹).连结QD,在新图形中,你发现
 是_______三角形.
是_______三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小泽和小超分别用掷A、B两枚骰子的方法来确定P(x,y)的位置,她们规定:小泽掷得的点数为x,小超掷得的点数为
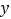 ,那么,她们各掷一次所确定的点落在已知直线y=-2x+6上的概率为( )
,那么,她们各掷一次所确定的点落在已知直线y=-2x+6上的概率为( )A.
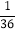 B.
B. 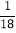 C.
C. 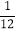 D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,C,D为线段AB上的两点,M,N分别是线段AC,BD的中点.
(1)如果CD=5cm,MN=8cm,求AB的长;
(2)如果AB=a,MN=b,求CD的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,O是直线AB上一点,OC为任意一条射线,OD平分∠BOC,OE平分∠AOC.
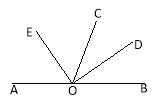
(1)指出图中∠AOD与∠BOE的补角;
(2)试判断∠COD与∠COE具有怎样的数量关系.并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知A、B两地相距4km,上午8:00时,亮亮从A地步行到B地,8:20时芳芳从B地出发骑自行车到A地,亮亮和芳芳两人离A地的距离S(km)与亮亮所用时间t(min)之间的函数关系如图所示,芳芳到达A地时间为( )
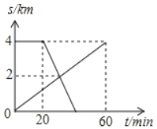
A. 8:30 B. 8:35 C. 8:40 D. 8:45
-
科目: 来源: 题型:
查看答案和解析>>【题目】2018年9月第22号台风“山竹”给某地造成严重影响.蓝天救援队驾着冲锋舟沿一条东西方向的河流营救灾民,早晨从
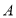 地出发,晚上最后到达
地出发,晚上最后到达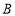 地,约定向东为正方向,当天航行依次记录如下(单位:千米):11,-6,15,-7,18,-8,10,-5,问:
地,约定向东为正方向,当天航行依次记录如下(单位:千米):11,-6,15,-7,18,-8,10,-5,问:(1)
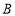 地在
地在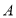 地的东面,还是西面?与
地的东面,还是西面?与 地相距多少千米?
地相距多少千米?(2)冲锋舟离开出发地最远是多少千米?
(3)若冲锋舟每千米耗油0.5升,油箱容量为30升,求途中至少需要补充多少升油?
相关试题

