【题目】已知方程组![]() 的解满足
的解满足![]() 为非正数,
为非正数,![]() 为负数.
为负数.
(1)求![]() 的取值范围;
的取值范围;
(2)化简:![]() ;
;
(3)在![]() 的取值范围内,当
的取值范围内,当![]() 为何整数时不等式
为何整数时不等式![]() 的解集为
的解集为![]() .
.
参考答案:
【答案】(1)-2<m≤3;(2)1-2m;(3)-1.
【解析】
(1)先求出方程组的解,根据x为非正数,y为负数,组成不等式组,解不等式组,即可解答.
(2)根据m的取值范围,绝对值的性质化简,即可解答.
(3)由不等式的性质求出m的范围,结合(1)中所求范围可得答案.
(1)解原方程组得:
![]() ,
,
∵x≤0,y<0,
∴![]() ,
,
解得-2<m≤3;
(2)|m-3|-|m+2|=3-m-m-2=1-2m;
(3)解不等式2mx+x<2m+1得(2m+1)x<2m+1,
∵x>1,
∴2m+1<0,
∴m<-![]() ,
,
∴-2<m<-![]() ,
,
∴m=-1.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知:在
 中,
中, ,
, .
.(1)按下列步骤用尺规作图(保留作图痕迹,不写出作法):作
 的平分线AD,交BC于D;
的平分线AD,交BC于D;(2)在(1)中,过点D作
 ,交AB于点E,若CD=4,则BC的长为 .
,交AB于点E,若CD=4,则BC的长为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】为加强中小学生安全和禁毒教育,某校组织了“防溺水、交通安全、禁毒”知识竞赛,为奖励在竞赛中表现优异的班级,学校准备从体育用品商场一次性购买若干个足球和篮球(每个足球的价格相同,每个篮球的价格相同),购买1个足球和1个篮球共需159元;足球单价是篮球单价的2倍少9元.
(1)求足球和篮球的单价各是多少元?
(2)根据学校实际情况,需一次性购买足球和篮球共20个,但要求购买足球和篮球的总费用不超过1550元,学校最多可以购买多少个足球?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,抛物线y= x2+bx+c与x轴、y轴分别相交于点A( 1,0)、B(0,3)两点,其顶点为D.
(1)求这条抛物线的解析式;
(2)若抛物线与x轴的另一个交点为E. 求△ODE的面积;抛物线的对称轴上是否存在点P使得△PAB的周长最短。若存在请求出P点的坐标,若不存在说明理由。

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图①,已知直线l1、l2,直线l3和直线l1、l2交于点C和D,在直线l3上有动点P(点P与点C、D不重合),点A在直线l1上,点B在直线l2上.
(1)如果点P在C、D之间运动时,且满足∠1+∠3=∠2,请写出l1与l2之间的位置关系 ;
(2)如图②如果l1∥l2,点P在直线l1的上方运动时,试猜想∠1+∠2与∠3之间关系并给予证明;
(3)如果l1∥l2,点P在直线l2的下方运动时,请直接写出∠PAC、∠PBD、∠APB之间的关系.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,过⊙O外一点P作⊙O的两条切线,切点分别为A、B,点M是劣弧AB上的任一点,过M作⊙0的切线分别交PA、PB于点C、D,过圆心O且垂直于OP的直线与PA、PB分别交于点E、F,那么
 的值为( )
的值为( )
A.
 B.
B.  C. 1 D. 2
C. 1 D. 2 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
 中,
中, 边的垂直平分线
边的垂直平分线 交
交 于点
于点 ,
, 边的垂直平分线
边的垂直平分线 交
交 于点
于点 ,
, 与
与 相交于点
相交于点 ,联结
,联结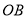 、
、 ,若
,若 的周长为
的周长为 ,
,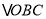 的周长为
的周长为 .
.
(1)求线段
 的长;
的长;(2)联结
 ,求线段
,求线段 的长;
的长;(3)若
 ,求
,求 的度数.
的度数.
相关试题

