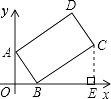
【题目】如图,矩形ABCD中,AB=2,BC=4,点A,B分别在y轴、x轴的正半轴上,点C在第一象限,如果∠OAB=30°,那么点C的坐标是 . 
参考答案:
【答案】(1+2 ![]() ,2)
,2)
【解析】解:∵AB=2,∠OAB=30°,
∴OB= ![]() AB=1,
AB=1,
在矩形ABCD中,∠ABC=90°,
∴∠OAB+∠ABO=90°,∠AB0+∠CBE=90°,
∴∠CBE=∠OAB=30°,
点C作CE⊥x轴于点E,
在Rt△BCE中,CE= ![]() BC=
BC= ![]() ×4=2,BE=
×4=2,BE= ![]() =
= ![]() =2
=2 ![]() ,
,
∴OE=OB+BE=1+2 ![]() ,
,
∴点C的坐标是(1+2 ![]() ,2).
,2).
故答案为:(1+2 ![]() ,2).
,2).
利用含30度角的直角三角形的性质得OB= 1,由矩形性质、同角的余角相等得∠CBE=∠OAB=30°从而得CE的长度,再利用勾股定理得BE的长度,从而得出C点的坐标。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是二次函数y=ax2+bx+c图象的一部分,图象过点A(﹣3,0),对称轴为直线x=﹣1,给出四个结论:
①c>0;
②若点B(﹣ ,y1)、C(﹣
,y1)、C(﹣  ,y2)为函数图象上的两点,则y1<y2;
,y2)为函数图象上的两点,则y1<y2;
③2a﹣b=0;
④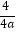 <0,
<0,
其中,正确结论的个数是( )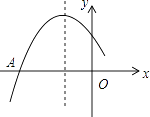
A.1
B.2
C.3
D.4 -
科目: 来源: 题型:
查看答案和解析>>【题目】如果点P(x,y)的坐标满足

(1)求点P的坐标.(用含m,n的式子表示x,y)
(2)如果点P在第二象限,且符合要求的整数只有两个,求n的范围.
(3)如果点P在第二象限,且所有符合要求的整数m之和为9,求n的范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】有
 筐白菜,以每筐
筐白菜,以每筐 千克为标准,超过或不足的分别用正、负来表示,记录如下:
千克为标准,超过或不足的分别用正、负来表示,记录如下:与标准质量的差
 单位:千克
单位:千克






筐 数






(1)与标准质量比较,
 筐白菜总计超过或不足多少千克?
筐白菜总计超过或不足多少千克?(2)若白菜每千克售价
 元,则出售这
元,则出售这 筐白菜可卖多少元?
筐白菜可卖多少元? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,边长为2的正方形ABCD内接于⊙O,过点D作⊙O的切线交BA延长线于点E,连接EO,交AD于点F,则EF长为 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
 面积为
面积为 ,第一次操作:分别延长
,第一次操作:分别延长 至点
至点 使
使 ,顺次连结
,顺次连结 ,得到
,得到 ,第二次操作:分别延长
,第二次操作:分别延长 至点
至点 ,使
,使 ,顺次连结
,顺次连结 ,得到
,得到 , ..按此规律,要使得到的三角形的面积超过
, ..按此规律,要使得到的三角形的面积超过 ,至少经过_________次操作.
,至少经过_________次操作.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,平面直角坐标系中,A1(1,1)、A2(﹣1,1)、A3(﹣1,﹣1)、A4(2,﹣1)、A5(2,2)、A6(﹣2,2)、A7(﹣2,﹣2)、A8(3,﹣2)、A9(3,3)、……、按此规律A2020的坐标为( )
A.(506,﹣505)B.(505,﹣504)C.(﹣504,﹣504)D.(﹣505,﹣505)
相关试题

