【题目】阅读以下材料,并按要求完成相应的任务.
在初中数学课本中重点介绍了提公因式法和运用公式法两种因式分解的方法,其中运用公式法即运用平方差公式:a2-b2=(a+b)(a-b)和完全平方公式:a2±2ab+b2=(a±b)2进行分解因式,能运用完全平方公式分解因式的多项式必须是三项式,其中有两项能写成两个数(或式)的平方和的形式,另一项是这两个数(或式)的积的2倍.当一个二次三项式不能直接运用完全平方公式分解因式时,可应用下面方法分解因式,先将多项式ax2+bx+c(a≠0)变形为a(x+m)2+n的形式,我们把这样的变形方法叫做多项式ax2+bx+c的配方法.再运用多项式的配方法及平方差公式能对一些多项式进行分解因式.
例如:x2+8x+7
=x2+8x+16-16+7
=(x+4)2-9
=(x+4+3)(x+4-3)
=(x+7)(x+1)
根据以上材料,完成相应的任务:
(1)利用“多项式的配方法”将x2+2x-3化成a(x+m)2+n的形式为_______;
(2)请你利用上述方法因式分解:
①x2+6x+8;
②x2-6x-7.
参考答案:
【答案】(1)![]() ;(2)①
;(2)①![]() ;②
;②![]()
【解析】
(1)将x+2x-3变成x+2x+1-4即可求得;
(2)①将x2+6x+8变为x2+6x+9-9+8的形式,再利用平方差即可进行因式分解;②将x2-6x-7变为x2-6x+9-9-7的形式再运用平方差即可进行因式分解;
解:(1)![]() =
=![]() =
=![]() ;
;
(2)①![]()
=![]()
=![]()
=![]()
=![]()
②![]()
=![]()
=![]()
=![]()
=![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,E是正方形ABCD边AB的中点,连接CE,过点B作BH⊥CE于F,交AC于G,交AD于H.下列说法:
 ;②点F是GB的中点;
;②点F是GB的中点;  ;
;  ,其中正确的结论的序号是_____________
,其中正确的结论的序号是_____________
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,△ABC三个顶点的坐标分别为:A(1,﹣4),B(5,﹣4),C(4,﹣1).
(1)将△ABC经过平移得到△A1B1C1,若点C的应点C1的坐标为(2,5),则点A,B的对应点A1,B1的坐标分别为 ;
(2)在如图的坐标系中画出△A1B1C1,并画出与△A1B1C1关于原点O成中心对称的△A2B2C2.

-
科目: 来源: 题型:
查看答案和解析>>【题目】计算
(1)(﹣7)﹣(+5)+(﹣4)﹣(﹣10);
(2)
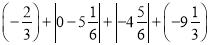 .
.(3)(﹣24)×(1+
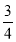 ﹣
﹣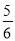 );
); (4)36÷(﹣3)2×(
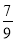 ﹣1)+(﹣1)3+(﹣1)2.
﹣1)+(﹣1)3+(﹣1)2. -
科目: 来源: 题型:
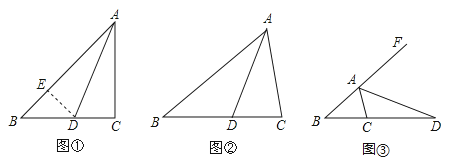
查看答案和解析>>【题目】在△ABC中,∠ACB=2∠B,(1)如图①,当∠C=90°,AD为∠ABC的角平分线时,在AB上截取AE=AC,连接DE,易证AB=AC+CD.请证明AB=AC+CD;
(2)①如图②,当∠C≠90°,AD为∠BAC的角平分线时,线段AB、AC、CD又有怎样的数量关系?请直接写出你的结论,不要求证明;
②如图③,当∠C≠90°,AD为△ABC的外角平分线时,线段AB、AC、CD又有怎样的数量关系?请写出你的猜想并证明.
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两名同学做摸球游戏,他们把四个分别标有1,2,3,4的大小和形状完全相同的小球放在一个不透明的口袋中.
(1)若从袋中随机摸出一球,则摸出的球的标号恰好是偶数的概率是 ;
(2)从袋中随机摸出一球后放回,摇匀后再随机摸出一球,若两次摸出的球的标号之和为偶数时,则甲胜;若两次摸出的球的标号之和为奇数时,则乙胜;试分析这个游戏是否公平?请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,有一块矩形铁皮,长110cm,宽70cm,在它的四角各切去一个同样的正方形,然后将四周突出部分折起,就能制作一个无盖的方盒,如果要制作的无盖的方盒的底面积为4500cm2,那么铁皮各角应切去的正方形边长是多少?

相关试题

