搜索
【题目】如图，E是正方形ABCD边AB的中点，连接CE，过点B作BH⊥CE于F，交AC于G，交AD于H．下列说法： 
；②点F是GB的中点； 
； 
，其中正确的结论的序号是_____________
参考答案：
【答案】①③④
【解析】解：∵四边形ABCD是正方形，∴AC平分∠HAB，∴ 
，故①正确；
假设F是GB的中点，∵CF⊥BG，∴CG=CB，∴CF平分∠BCG．而CE是Rt△ABC的中线，∴CE不能平分∠BCA，矛盾，故F是GB的中点是错误的．故②错误；
易证△HAB≌△EBC，∴HA=EB=
AB．过G作GM⊥AB于M．∵∠CAB=45°，∴△AMG是等腰直角三角形，∴AM=MG，AG=
MG，∵GM⊥AB，HA⊥AB，∴GM∥HA，∴△GBM∽△HBA，∴
．∵AH=
AB，∴GM=
AB，∴AG=
AB．故③正确；
由①③得：GB=2HG，∴BH=3HG，∴S△HAB=3S△AHG．∵△HAB≌△EBC，∴S△HAB=S△EBC=
S△ABC，∴S△HAB=
S△ABC．故④正确．
故①③④正确．
-
科目： 来源： 题型：
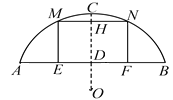
查看答案和解析>>【题目】如图，某地有一座圆弧形的拱桥，桥下水面宽为7.2m，拱顶高出水面2.4m，现有一艘宽3m，船舱顶部为正方形并高出水面2m的货船要经过这里，此时货船能顺利通过这座拱桥吗？请说明理由．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，已知A，B，C是数轴上三点，点C表示的数为6，BC＝4，AB＝12．
(1)写出数轴上点A，B表示的数．
(2)动点P，Q分别从A，C同时出发，点P以每秒6个单位长度的速度沿数轴向右匀速运动，点Q以每秒3个单位长度的速度沿数轴向左匀速运动．若M为AP的中点，点N在线段CQ上，且CN＝
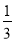CQ，设运动时间为ts(t＞0)．①写出数轴上点M，N表示的数(用含t的式子表示)．
②t为何值时，原点O恰为线段PQ的中点?
-
科目： 来源： 题型：
查看答案和解析>>【题目】同学们都知道，
表示5与 -2之差的绝对值，实际上也可以理解为 5 与 -2两数在数轴上所对的两点之间的距离，则使得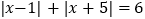
这样的整数
有____个． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在平面直角坐标系中，△ABC三个顶点的坐标分别为：A（1，﹣4），B（5，﹣4），C（4，﹣1）．
（1）将△ABC经过平移得到△A1B1C1，若点C的应点C1的坐标为（2，5），则点A，B的对应点A1，B1的坐标分别为 ；
（2）在如图的坐标系中画出△A1B1C1，并画出与△A1B1C1关于原点O成中心对称的△A2B2C2．
-
科目： 来源： 题型：
查看答案和解析>>【题目】计算
（1）（﹣7）﹣（+5）+（﹣4）﹣（﹣10）；
（2）
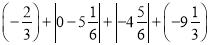.（3）（﹣24）×（1+
﹣
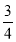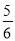）； （4）36÷（﹣3）2×（
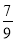﹣1）+（﹣1）3+（﹣1）2． -
科目： 来源： 题型：
查看答案和解析>>【题目】阅读以下材料，并按要求完成相应的任务．
在初中数学课本中重点介绍了提公因式法和运用公式法两种因式分解的方法，其中运用公式法即运用平方差公式：a2-b2=（a+b）（a-b）和完全平方公式：a2±2ab+b2=（a±b）2进行分解因式，能运用完全平方公式分解因式的多项式必须是三项式，其中有两项能写成两个数（或式）的平方和的形式，另一项是这两个数（或式）的积的2倍．当一个二次三项式不能直接运用完全平方公式分解因式时，可应用下面方法分解因式，先将多项式ax2+bx+c（a≠0）变形为a（x+m）2+n的形式，我们把这样的变形方法叫做多项式ax2+bx+c的配方法．再运用多项式的配方法及平方差公式能对一些多项式进行分解因式．
例如：x2+8x+7
=x2+8x+16-16+7
=(x+4）2-9
=(x+4+3)(x+4-3)
=(x+7)(x+1)
根据以上材料，完成相应的任务：
（1）利用“多项式的配方法”将x2+2x-3化成a（x+m）2+n的形式为_______；
（2）请你利用上述方法因式分解：
①x2+6x+8；
②x2-6x-7．
相关试题
