搜索
【题目】如图，在Rt△ABC中，∠ACB=90°，AC=6，BC=8，AB=10，AD是∠BAC的平分线．若P，Q分别是AD和AC上的动点，则PC+PQ的最小值是（ ）
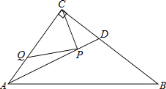
A. 2.4 B. 4.8 C. 4 D. 5
参考答案：
【答案】B
【解析】
过点C作CM⊥AB交AB于点M，交AD于点P，过点P作PQ⊥AC于点Q，由AD是∠BAC的平分线．得出PQ=PM，这时PC+PQ有最小值，即CM的长度，运用勾股定理求出AB，再运用S△ABC=
ABCM=ACBC，得出CM的值，即PC+PQ的最小值．
如图，过点C作CM⊥AB交AB于点M，交AD于点P，过点P作PQ⊥AC于点Q，
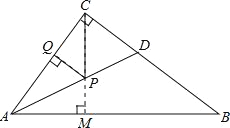
∵AD是∠BAC的平分线.
∴PQ=PM，这时PC+PQ有最小值，即CM的长度,
∵AC=6,BC=8,∠ACB=90°,
∴AB=
,
∵
=ABCM=ACBC,
∴CM=
.
故选：B.
-
科目： 来源： 题型：
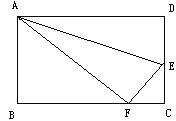
查看答案和解析>>【题目】如图所示，折叠长方形一边AD，点D落在BC边的点F处， 已知BC=10厘米，AB=8厘米，求FC和EF的长.
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在平面直角坐标系中，点A，B的坐标分别为（－1，0），（3，0），现同时将点A，B分别向上平移2个单位，再向右平移1个单位，分别得到点A，B的对应点C，D，连接AC，BD，CD．
（1）求点C，D的坐标及平行四边形ABDC的面积
.（2）在y轴上是否存在一点P，连接PA，PB，使
＝2，若存在这样一点，求出点P的坐标，若不存在，试说明理由． （3）点P是四边形ABCD边上的点，若△OPC为等腰三角形时，直接写出点P的坐标．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，等腰△ABC中，AB=AC，AB的垂直平分线MN交AC于点D，∠DBC=15°，则∠A的度数是（ ）
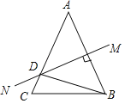
A. 50° B. 45° C. 55° D. 60°
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在
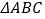中，AB=AC，∠BAC=90
，直角∠EPF的顶点是BC的中点，两边PE，PF分别交AB，AC于点E，F．给出以下五个结论：（1）AE=CF；（2）∠APE =∠CPF；（3）△EPF是等腰直角三角形；（4）
=
（5）EF=AP其中一定成立的有________个．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，AB，BC，CD分别与⊙O相切于E，F，G．且AB∥CD．BO=6cm，CO=8cm．
（1）求证：BO⊥CO；
（2）求BE和CG的长． -
科目： 来源： 题型：
查看答案和解析>>【题目】二次函数图象的顶点在原点O，经过点A（1，
）；点F（0，1）在y轴上．直线y=﹣1与y轴交于点H．
（1）求二次函数的解析式；
（2）点P是（1）中图象上的点，过点P作x轴的垂线与直线y=﹣1交于点M，求证：FM平分∠OFP；
（3）当△FPM是等边三角形时，求P点的坐标．
相关试题
