搜索
【题目】如图，等腰△ABC中，AB=AC，AB的垂直平分线MN交AC于点D，∠DBC=15°，则∠A的度数是（ ）
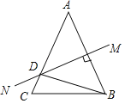
A. 50° B. 45° C. 55° D. 60°
参考答案：
【答案】A
【解析】
根据线段垂直平分线上的点到两端点的距离相等可得AD=BD，根据等边对等角可得∠A=∠ABD，然后表示出∠ABC，再根据等腰三角形两底角相等可得∠C=∠ABC，然后根据三角形的内角和定理列出方程求解即可．
∵MN 是 AB 的垂直平分线,
∴AD=BD ，
∴∠A=∠ABD .
∵∠DBC=15° .
∴∠ABC=∠A+15°.
∵AB=AC ,
∴∠C=∠ABC=∠A+15°.
∴∠A+∠A+15°+∠A+15°=180° .
解得 ∠A=50°.
故选：A.
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，一艘海轮在A点时测得灯塔C在它的北偏东42°方向上，它沿正东方向航行80海里后到达B处，此时灯塔C在它的北偏西55°方向上．
（1）求海轮在航行过程中与灯塔C的最短距离（结果精确到0.1）；
（2）求海轮在B处时与灯塔C的距离（结果保留整数）．
（参考数据：sin55°≈0.819，cos55°≈0.574，tan55°≈1.428，tan42°≈0.900，tan35°≈0.700，tan48°≈1.111） -
科目： 来源： 题型：
查看答案和解析>>【题目】如图所示，折叠长方形一边AD，点D落在BC边的点F处， 已知BC=10厘米，AB=8厘米，求FC和EF的长.
-
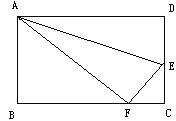
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在平面直角坐标系中，点A，B的坐标分别为（－1，0），（3，0），现同时将点A，B分别向上平移2个单位，再向右平移1个单位，分别得到点A，B的对应点C，D，连接AC，BD，CD．
（1）求点C，D的坐标及平行四边形ABDC的面积
.（2）在y轴上是否存在一点P，连接PA，PB，使
＝2，若存在这样一点，求出点P的坐标，若不存在，试说明理由． （3）点P是四边形ABCD边上的点，若△OPC为等腰三角形时，直接写出点P的坐标．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在Rt△ABC中，∠ACB=90°，AC=6，BC=8，AB=10，AD是∠BAC的平分线．若P，Q分别是AD和AC上的动点，则PC+PQ的最小值是（ ）
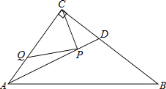
A. 2.4 B. 4.8 C. 4 D. 5
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在
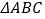中，AB=AC，∠BAC=90
，直角∠EPF的顶点是BC的中点，两边PE，PF分别交AB，AC于点E，F．给出以下五个结论：（1）AE=CF；（2）∠APE =∠CPF；（3）△EPF是等腰直角三角形；（4）
=
（5）EF=AP其中一定成立的有________个．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，AB，BC，CD分别与⊙O相切于E，F，G．且AB∥CD．BO=6cm，CO=8cm．
（1）求证：BO⊥CO；
（2）求BE和CG的长．
相关试题
