【题目】二次函数图象的顶点在原点O,经过点A(1, ![]() );点F(0,1)在y轴上.直线y=﹣1与y轴交于点H.
);点F(0,1)在y轴上.直线y=﹣1与y轴交于点H.
(1)求二次函数的解析式;
(2)点P是(1)中图象上的点,过点P作x轴的垂线与直线y=﹣1交于点M,求证:FM平分∠OFP;
(3)当△FPM是等边三角形时,求P点的坐标.
参考答案:
【答案】
(1)
解:∵二次函数图象的顶点在原点O,
∴设二次函数的解析式为y=ax2,
将点A(1, ![]() )代入y=ax2得:a=
)代入y=ax2得:a= ![]() ,
,
∴二次函数的解析式为y= ![]() x2
x2
(2)
证明:∵点P在抛物线y= ![]() x2上,
x2上,
∴可设点P的坐标为(x, ![]() x2),
x2),
过点P作PB⊥y轴于点B,则BF=| ![]() x2﹣1|,PB=|x|,
x2﹣1|,PB=|x|,
∴Rt△BPF中,
PF= ![]() =
= ![]() x2+1,
x2+1,
∵PM⊥直线y=﹣1,
∴PM= ![]() x2+1,
x2+1,
∴PF=PM,
∴∠PFM=∠PMF,
又∵PM∥y轴,
∴∠MFH=∠PMF,
∴∠PFM=∠MFH,
∴FM平分∠OFP
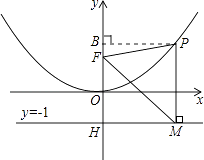
(3)
解:当△FPM是等边三角形时,∠PMF=60°,
∴∠FMH=30°,
在Rt△MFH中,MF=2FH=2×2=4,
∵PF=PM=FM,
∴ ![]() x2+1=4,
x2+1=4,
解得:x=±2 ![]() ,
,
∴ ![]() x2=
x2= ![]() ×12=3,
×12=3,
∴满足条件的点P的坐标为(2 ![]() ,3)或(﹣2
,3)或(﹣2 ![]() ,3)
,3)
【解析】(1)根据题意可设函数的解析式为y=ax2 , 将点A代入函数解析式,求出a的值,继而可求得二次函数的解析式;(2)过点P作PB⊥y轴于点B,利用勾股定理求出PF,表示出PM,可得PF=PM,∠PFM=∠PMF,结合平行线的性质,可得出结论;(3)首先可得∠FMH=30°,设点P的坐标为(x, ![]() x2),根据PF=PM=FM,可得关于x的方程,求出x的值即可得出答案.
x2),根据PF=PM=FM,可得关于x的方程,求出x的值即可得出答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠ACB=90°,AC=6,BC=8,AB=10,AD是∠BAC的平分线.若P,Q分别是AD和AC上的动点,则PC+PQ的最小值是( )
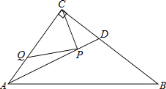
A. 2.4 B. 4.8 C. 4 D. 5
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
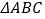 中,AB=AC,∠BAC=90
中,AB=AC,∠BAC=90 ,直角∠EPF的顶点是BC的中点,两边PE,PF分别交AB,AC于点E,F.给出以下五个结论:(1)AE=CF;(2)∠APE =∠CPF;(3)△EPF是等腰直角三角形;(4)
,直角∠EPF的顶点是BC的中点,两边PE,PF分别交AB,AC于点E,F.给出以下五个结论:(1)AE=CF;(2)∠APE =∠CPF;(3)△EPF是等腰直角三角形;(4) =
=
 (5)EF=AP其中一定成立的有________个.
(5)EF=AP其中一定成立的有________个.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB,BC,CD分别与⊙O相切于E,F,G.且AB∥CD.BO=6cm,CO=8cm.

(1)求证:BO⊥CO;
(2)求BE和CG的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中BA=BC,点D是AB延长线上一点,DF⊥AC于F交BC于E,
求证:△DBE是等腰三角形.

-
科目: 来源: 题型:
查看答案和解析>>【题目】数学活动课上,老师准备了若干个如图1的三种纸片,A种纸片边长为a的正方形,B种纸片是边长为b的正方形,C种纸片长为a、宽为b的长方形.并用A种纸片一张,B种纸片张,C种纸片两张拼成如图2的大正方形.

(1)请用两种不同的方法求图2大正方形的面积.
方法1: ;方法2:
(2)观察图2,请你写出下列三个代数式:(a+b)2,a2+b2,ab之间的等量关系.
(3)根据(2)题中的等量关系,解决如下问题:
①已知:a+b=5,a2+b2=11,求ab的值;
②已知(2018﹣a)2+(a﹣2017)2=5,求(2018﹣a)(a﹣2017)的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算下列各题
(1)计算:(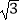 ﹣2)0+(﹣1)2014+
﹣2)0+(﹣1)2014+ 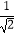 ﹣sin45°;
﹣sin45°;
(2)先化简,再求值:(a2b+ab)÷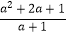 ,其中a=
,其中a= 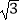 +1,b=
+1,b= 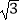 ﹣1.
﹣1.
相关试题

