【题目】已知![]() 港口位于
港口位于![]() 观测点北偏东
观测点北偏东![]() 方向,且其到
方向,且其到![]() 观测点正北方向的距离
观测点正北方向的距离![]() 的长为
的长为![]() ,一艘货轮从
,一艘货轮从![]() 港口以
港口以![]() 的速度沿如图所示的
的速度沿如图所示的![]() 方向航行,
方向航行,![]() 后达到
后达到![]() 处,现测得
处,现测得![]() 处位于
处位于![]() 观测点北偏东
观测点北偏东![]() 方向,求此时货轮与
方向,求此时货轮与![]() 观测点之间的距离
观测点之间的距离![]() 的长(精确到
的长(精确到![]() ).(参考数据:
).(参考数据:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() )
)

参考答案:
【答案】此时货轮与![]() 观测点之间的距离
观测点之间的距离![]() 约为
约为![]() .
.
【解析】
根据在Rt△ADB中,sin∠DBA=![]() ,得出AB的长,进而得出tan∠BAH=
,得出AB的长,进而得出tan∠BAH=![]() ,求出BH的长,即可得出AH以及CH的长,进而得出答案.
,求出BH的长,即可得出AH以及CH的长,进而得出答案.
BC=40×![]() =10,
=10,
在Rt△ADB中,sin∠DBA=![]() ,sin53.2°≈0.8,
,sin53.2°≈0.8,
所以AB=![]() =20,
=20,
如图,过点B作BH⊥AC,交AC的延长线于H,
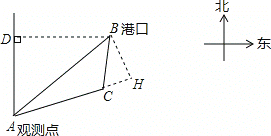
在Rt△AHB中,∠BAH=∠DAC-∠DAB=63.6°-37°=26.6°,
tan∠BAH=![]() ,0.5=
,0.5=![]() ,AH=2BH,
,AH=2BH,
BH2+AH2=AB2,BH2+(2BH)2=202,BH=4![]() ,所以AH=8
,所以AH=8![]() ,
,
在Rt△BCH中,BH2+CH2=BC2,CH=2![]() ,
,
所以AC=AH-CH=8![]() -2
-2![]() =6
=6![]() ≈13.4,
≈13.4,
答:此时货轮与A观测点之间的距离AC约为13.4km.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(9分)如图所示,某数学活动小组选定测量小河对岸大树BC的高度,他们在斜坡上D处测得大树顶端B的仰角是30,朝大树方向下坡走6米到达坡底A处,在A处测得大树顶端B的仰角是48°. 若坡角∠FAE=30°,求大树的高度. (结果保留整数,参考数据:sin48°≈0.74,cos48°≈0.67,tan48°≈1.11,
 ≈1.73)
≈1.73)
-
科目: 来源: 题型:
查看答案和解析>>【题目】规定:在平面直角坐标系中,如果点P的坐标为(m,n),向量
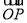 可以用点P的坐标表示为:
可以用点P的坐标表示为: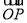 =(m,n).已知
=(m,n).已知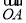 =(x1,y1),
=(x1,y1),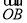 =(x2,y2),如果x1x2+y1y2=0,那么
=(x2,y2),如果x1x2+y1y2=0,那么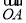 与
与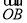 互相垂直,在下列四组向量中,互相垂直的是( )
互相垂直,在下列四组向量中,互相垂直的是( )A.
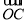 =(3,20190),
=(3,20190),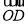 =(﹣3﹣1,1)
=(﹣3﹣1,1)B.
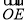 =(
=(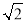 ﹣1,1),
﹣1,1), =(
=(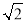 +1,1)
+1,1)C.
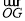 =(
=(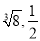 ),
),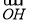 =((﹣
=((﹣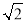 )2,8)
)2,8)D.
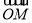 =(
=(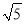 +2,
+2,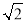 ),
),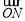 =(
=(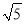 ﹣2,
﹣2,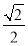 )
) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一艘船以每小时
 海里的速度自
海里的速度自 向正北方向航行,船在
向正北方向航行,船在 处时,灯塔
处时,灯塔 在船的北偏东
在船的北偏东 ,航行
,航行 小时后到
小时后到 处,此时灯塔
处,此时灯塔 在船的北偏东
在船的北偏东 ,(运算结果保留根号)
,(运算结果保留根号) 求船在
求船在 处时与灯塔
处时与灯塔 的距离;
的距离; 若船从
若船从 处继续向正北方向航行,问经过多长时间船与灯塔
处继续向正北方向航行,问经过多长时间船与灯塔 的距离最近.
的距离最近.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
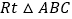 中,
中, ,点
,点 、
、 分别为
分别为 的外心和内心,
的外心和内心, ,
, ,则
,则 的值为( )
的值为( )
A.
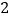 B.
B.  C.
C. 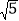 D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,点A1,A2,A3,…分别在x轴上,点B1,B2,B3,…分别在直线y=x上,△OA1B1,△B1A1A2,△B1B2A2,△B2A2A3,△B2B3A3…,都是等腰直角三角形,如果OA1=1,则点A2019的坐标为_____.
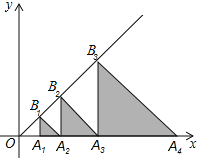
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,三角形BCO是三角形BAO经过某种变换得到的.
(1)写出A,C的坐标;
(2)图中A与C的坐标之间的关系是什么?
(3)如果三角形AOB中任意一点M的坐标为(x,y),那么它的对应点N的坐标是什么?

相关试题

