【题目】Rt△ABC中,∠C=90°,点D,E分别是△ABC边AC,BC上的点,点P是一动点.令∠PDA=∠1,∠PEB=∠2,∠DPE=∠α.
(1)若点P在线段AB上,如图①所示,且∠α=50°,则∠1+∠2=________°;
(2)若点P在边AB上运动,如图②所示,则∠α,∠1,∠2之间的关系为:____________;

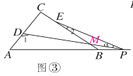
(3)若点P运动到边AB的延长线上,如图③所示,则∠α,∠1,∠2之间有何关系?猜想并说明理由;

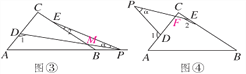
(4)若点P运动到△ABC形外,如图④所示,则∠α,∠1,∠2之间的关系为:____________.
参考答案:
【答案】(1)140;(2) 90°+∠α.(3)90°+∠2+∠α.;(4)90°+∠1-∠α.
【解析】试题分析:(1)根据四边形内角和定理以及邻补角的定义,得出∠1+∠2=∠C+∠α,进而得出即可;
(2)利用(1)中所求的结论得出∠α、∠1、∠2之间的关系即可;
(3)利用三角外角的性质,得出∠1=∠C+∠2+α=90°+∠2+α;
(4)利用三角形内角和定理以及邻补角的性质可得出∠α、∠1、∠2之间的关系.
试题分析:(1)∵∠1+∠2+∠CDP+∠CEP=360°,∠C+∠α+∠CDP+∠CEP=360°,
∴∠1+∠2=∠C+∠α,
∵∠C=90°,∠α=50°,
∴∠1+∠2=140°,
故答案为:140;
(2)由(1)得∠α+∠C=∠1+∠2,
∴∠1+∠2=90°+∠α.
故答案为:∠1+∠2=90°+∠α.
(3)∠1=90°+∠2+∠α.理由如下:如图③,
设DP与BE的交点为M,
∵∠2+∠α=∠DME,∠DME+∠C=∠1,
∴∠1=∠C+∠2+∠α=90°+∠2+∠α.
(4)如图④,
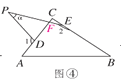
设PE与AC的交点为F,
∵∠PFD=∠EFC,
∴180°-∠PFD=180°-∠EFC,
∴∠α+180°-∠1=∠C+180°-∠2,
∴∠2=90°+∠1-∠α.
故答案为:∠2=90°+∠1-∠α
-
科目: 来源: 题型:
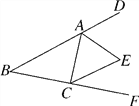
查看答案和解析>>【题目】如图,在△ABC中,∠B=40°,△ABC的外角∠DAC和∠ACF的平分线交于点E,求∠AEC的度数.
-
科目: 来源: 题型:
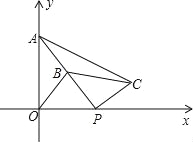
查看答案和解析>>【题目】如图,在平面直角坐标系中,点A的坐标为(0,2),点P(t,0)在x轴上,B是线段PA的中点.将线段PB绕着点P顺时针方向旋转90°,得到线段PC,连结OB、BC.
(1)判断△PBC的形状,并简要说明理由;
(2)当t>0时,试问:以P、O、B、C为顶点的四边形能否为平行四边形?若能,求出相应的t的值?若不能,请说明理由;
(3)当t为何值时,△AOP与△APC相似?
-
科目: 来源: 题型:
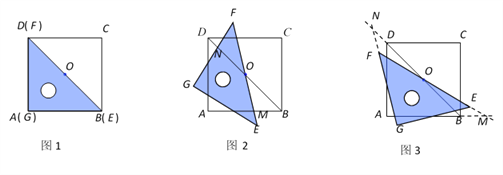
查看答案和解析>>【题目】如图1,一等腰直角三角尺GEF的两条直角边与正方形ABCD的两条边分别重合在一起.现正方形ABCD保持不动,将三角尺GEF绕斜边EF的中点O(点O也是BD中点)按顺时针方向旋转.
(1)如图2,当EF与AB相交于点M,GF与BD相交于点N时,通过观察或测量BM,FN的长度,猜想BM,FN满足的数量关系,并证明你的猜想;
(2)若三角尺GEF旋转到如图3所示的位置时,线段FE的延长线与AB的延长线相交于点M,线段BD的延长线与GF的延长线相交于点N,此时,(1)中的猜想还成立吗?若成立,请证明;若不成立,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,每个小正方形的边长为1个单位,每个小方格的顶点叫格点.
⑴画出△ABC向右平移4个单位后得到的△A1B1C1;
⑵图中AC与A1C1的关系是: ;
⑶画出△ABC中AB边上的中线CD;
⑷△ACD的面积为 .

-
科目: 来源: 题型:
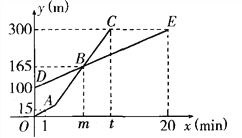
查看答案和解析>>【题目】小强和爸爸上山游玩,两人距地面的高度y(m)与小强登山时间x(min)之间的函数图像分别如图中折线OAC(小强)和线段DE(爸爸)所示,根据函数图像进行以下探究:
(1)爸爸登山的速度是每分钟_______m;
(2)请解释图中点B的实际意义;
(3)求线段DE所表示的y与x之间的函数关系式,并写出自变量x的取值范围;
(4)求m的值;
(5)若小强提速后,他登山的速度是爸爸速度的3倍,试问小强登山多长时间时开始提速?此时小强距地面的高度是多少米?
-
科目: 来源: 题型:
查看答案和解析>>【题目】按要求解一元二次方程
(1)4x2﹣8x+1=0(配方法) (2)7x(5x+2)=6(5x+2)(因式分解法)
(3)3x2+5(2x+1)=0(公式法) (4)x2﹣2x﹣8=0.
相关试题

