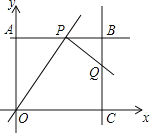
【题目】如图,在平面直角坐标系中,四边形OABC为矩形,点A、点C分别在y轴、x轴的正半轴上,OA,OC的长分别是方程x2-7x+12=0的两根(OA<OC).P为直线AB上一动点,直线PQ⊥OP交直线BC于点Q.
(1)求点B的坐标;
(2)当点P在线段AB上运动(不与A,B重合)时,设点P的横坐标为m,线段CQ的长度为l.求出l关于m的函数解析式;
(3)在坐标平面内是否存在点D,使以O、P、Q、D为顶点的四边形为正方形?若存在,请直接写出D点的坐标;若不存在,请说明理由.
参考答案:
【答案】(1)B(4,3);(2) ![]() ;(3)存在,D(3,-1)或(-3,7).
;(3)存在,D(3,-1)或(-3,7).
【解析】
(1)通过解方程求出线段的长度,利用矩形的性质得到AB=4,BC=3,求得B(4,3);
(2)因为点P在线段AB上,点P的横坐标为m,用m表示出AP的长度,利用相似三角形的性质列出比例式求出l关于m的函数解析式;
(3)如图,过点D作DE⊥OC于E,由以O、P、Q、D为顶点的四边形为正方形,得到OP=PQ=OD,通过三角形全等,对应边相等求得AP=m=1,再根据另一对三角形全等得到点D的坐标.
(1)解方程x2-7x+12=0得:x1=3,x2=4,
∴OA=3,OC=4,
∴A(0,3),C(4,0),
∵四边形OABC为矩形,
∴AB=4,BC=3,
∴B(4,3);
(2)点P在线段AB上,点P的横坐标为m,
∴AP=m,
∵CQ=l,
∴BQ=3-l,
∵∠OAP=∠B=∠OPQ=90°,
∴∠APO+∠BPQ=∠APO+∠AOP=90°,
∴∠APO=∠BPQ,
∴△APO∽△BPQ,
∴![]() ,
,
即![]() ,
,
∴![]() ;
;
(3)存在,
如图,过点D作DE⊥OC于E,
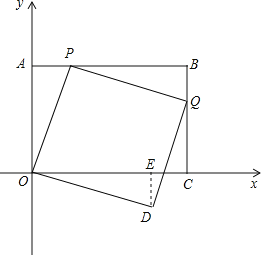
∵四边形ODQP是正方形,
∴OP=PQ=OD,
在△AOP与△BPQ中,
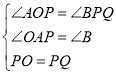 ,
,
∴△AOP≌△BPQ(AAS),
∴PB=OA=3,
∴AP=BP=1,
在△AOP与△OED中,
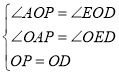 ,
,
∴△AOP≌△OEP(AAS),
∴OE=AO=3,DE=AP=1,
∴D(3,-1).
若点P在点B的右边,同理可得D(-3,7)
综上所述D(3,-1)或(-3,7)
-
科目: 来源: 题型:
查看答案和解析>>【题目】有这样一个问题:探究函数
 的图象与性质.小东根据学习函数的经验,对函数
的图象与性质.小东根据学习函数的经验,对函数 的图象与性质进行了探究.下面是小东的探究过程,请补充完整:
的图象与性质进行了探究.下面是小东的探究过程,请补充完整:(1)函数
 的自变量x的取值范围是 ;
的自变量x的取值范围是 ;(2)下表是x与y的几组对应值.

...







1
2
3
...

...








m
...
求m的值;
(3)如图,在平面直角坐标系中,已描出了以上表中各对对应值为坐标的点.根据描出的点,画出该函数的图象;

(4)进一步探究发现,该函数图象在第一象限内的最低点的坐标是(1,
 ).结合函数的图象,写出该函数的其它性质(写两条即可).
).结合函数的图象,写出该函数的其它性质(写两条即可). -
科目: 来源: 题型:
查看答案和解析>>【题目】计算:(1)﹣15﹣(﹣8)+(﹣11)﹣12
(2)(﹣3)×(﹣4)﹣15÷

(3)
 ×36
×36(4)﹣22+3×(﹣1)4﹣(﹣4)×5
-
科目: 来源: 题型:
查看答案和解析>>【题目】观察与思考:阅读下列材料,并解决后面的问题
在锐角△ABC中,∠A、∠B、∠C的对边分别是a、b、c,过A作AD⊥BC于D(如图(1)),则
 ,即AD=csinB,AD=bsinC,于是csinB=bsinC,即
,即AD=csinB,AD=bsinC,于是csinB=bsinC,即 ,同理有:
,同理有:  ,所以
,所以 .
.即:在一个锐角三角形中,各边和它所对角的正弦的比相等在锐角三角形中,若已知三个元素(至少有一条边),运用上述结论和有关定理就可以求出其余三个未知元素.
根据上述材料,完成下列各题.

(1)如图(2),△ABC中,∠B=45°,∠C=75°,BC=60,则∠A= ;AC= ;
(2)某次巡逻中,如图(3),我渔政船在C处测得钓鱼岛A在我渔政船的北偏西30°的方向上,随后以40海里/时的速度按北偏东30°的方向航行,半小时后到达B处,此时又测得钓鱼岛A在的北偏西75°的方向上,求此时渔政船距钓鱼岛A的距离AB.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形ABCD中,DC∥AB,AD=5,CD=3,sinA=sinB=
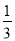 ,动点P自A点出发,沿着边AB向点B匀速运动,同时动点Q自点A出发,沿着边AD﹣DC﹣CB匀速运动,速度均为每秒1个单位,当其中一个动点到达终点时,它们同时停止运动,设点P运动t(秒)时,△APQ的面积为s,则s关于t的函数图象是( )
,动点P自A点出发,沿着边AB向点B匀速运动,同时动点Q自点A出发,沿着边AD﹣DC﹣CB匀速运动,速度均为每秒1个单位,当其中一个动点到达终点时,它们同时停止运动,设点P运动t(秒)时,△APQ的面积为s,则s关于t的函数图象是( )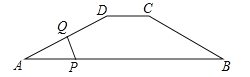
A.
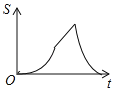 B.
B. 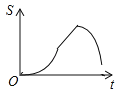
C.
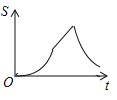 D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在数轴上点A,B,C表示的数分别为﹣2,0,6.点A与点B之间的距离表示为AB,点B与点C之间的距离表示为BC,点A与点C之间的距离表示为AC.
(1)AB= ,BC= ,AC= ;
(2)点A,B,C开始在数轴上运动,若点A以每秒1个单位长度的速度向左运动,同时点B和点C分别以每秒2个单位长度和5个单位长度的速度向右运动.
①设运动时间为t,请用含有t的算式分别表示出AB,BC,AC;
②在①的条件下,请问:BC﹣AB的值是否随着运动时间t的变化而变化?若变化,请说明理由:若不变,请求其值.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某景区的门票销售分两类:一类为散客门票,价格为
 元/张;另一类为团体门票(一次性购买门票
元/张;另一类为团体门票(一次性购买门票 张以上),每张门票价格在散客门票价格的基础上打
张以上),每张门票价格在散客门票价格的基础上打 折,某班部分同学要去该景点旅游,设参加旅游
折,某班部分同学要去该景点旅游,设参加旅游 人,购买门票需要
人,购买门票需要 元
元(1)如果每人分别买票,求
 与
与 之间的函数关系式:
之间的函数关系式:(2)如果购买团体票,求
 与
与 之间的函数关系式,并写出自变量的取值范围;
之间的函数关系式,并写出自变量的取值范围;(3)请根据人数变化设计一种比较省钱的购票方式.
相关试题

