搜索
【题目】某班将举行“数学知识竞赛”活动，班长安排小明购买奖品，下面两图是小明买回奖品时与班长的对话情境：
请根据上面的信息，解决问题：
(1)试计算两种笔记本各买了多少本？
(2)请你解释：小明为什么不可能找回68元？
参考答案：
【答案】(1) 5元笔记本买了25本，8元笔记本买了15本 (2)不可能找回68元
【解析】试题分析：（1）解法一：设5元、8元的笔记本分别买
本，
本，
依题意，得：
，解得：
.
答：5元和8元笔记本分别买了25本和15本.
解法二：设买本5元的笔记本，则买（40－）本8元笔记本，依题意，得：
，解得：=25.
答：：5元和8元笔记本分别买了25本和15本.
（2）解法一：应找回的钱款为300－5×25－8×15=55≠68，故不能找回68元.
解法二：设买
本5元的笔记本，则买
本8元的笔记本.依题意，得：
，解得
.因是正整数，所以不合题意，应舍去，故不能找回68元.
解法三：买25本5元的笔记本和15本8元的笔记本的价钱总数应为奇数而不是偶数，故不能找回68元.
-
科目： 来源： 题型：
查看答案和解析>>【题目】计算：（2a+5）（a-3）=______．
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知a，b，c为一个三角形的三条边长，且方程
有两个相等的实数根，试判断这个三角形的形状。 -
科目： 来源： 题型：
查看答案和解析>>【题目】定义：如图①，抛物线y＝ax2＋bx＋c(a≠0)与x轴交于A，B两点，点P在该抛物线上(P点与A、B两点不重合)．如果△ABP的三边满足AP2＋BP2＝AB2，则称点P为抛物线y＝ax2＋bx＋c(a≠0)的勾股点．
(1)直接写出抛物线y＝－x2＋1的勾股点的坐标．
(2)如图②，已知抛物线y＝ax2＋bx(a≠0)与x轴交于A，B两点，点P(1，
)是抛物线的勾股点，求抛物线的函数表达式．(3)在(2)的条件下，点Q在抛物线上，求满足条件S△ABQ＝S△ABP的Q点(异于点P)的坐标．
-
科目： 来源： 题型：
查看答案和解析>>【题目】某蔬菜加工公司先后两批次收购蒜薹(tái)共100吨．第一批蒜薹价格为4000元/吨；因蒜薹大量上市，第二批价格跌至1000元/吨．这两批蒜薹共用去16万元．
(1)求两批次购进蒜薹各多少吨；
(2)公司收购后对蒜薹进行加工，分为粗加工和精加工两种：粗加工每吨利润400元，精加工每吨利润1000元．要求精加工数量不多于粗加工数量的三倍．为获得最大利润，精加工数量应为多少吨？最大利润是多少？
-
科目： 来源： 题型：
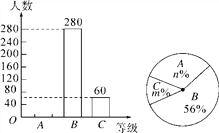
查看答案和解析>>【题目】某报社为了解市民对“社会主义核心价值观”的知晓程度，采取随机抽样的方式进行问卷调查，调查结果分为“A.非常了解”、“B.了解”、“C.基本了解”三个等级，并根据调查结果绘制了如下两幅不完整的统计图．
(1)这次调查的市民人数为________人，m＝________，n＝________；
(2)补全条形统计图；
(3)若该市约有市民100000人，请你根据抽样调查的结果，估计该市大约有多少人对“社会主义核心价值观”达到“A.非常了解”的程度．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，抛物线y1=
（x+1）2+1与y2=a（x﹣4）2﹣3交于点A（1，3），过点A作x轴的平行线，分别交两条抛物线于B、C两点，且D、E分别为顶点．则下列结论：①a=
；②AC=AE；③△ABD是等腰直角三角形；④当x＞1时，y1＞y2 其中正确结论的个数是（ )
A. 1个B．2个C．3个D．4个
相关试题
