【题目】已知,点C在以AB为直径的半圆上,∠CAB的平分线AD交BC于点D,⊙O经过A、D两点,且圆心O在AB上.
(1)求证:BD是⊙O的切线.
(2)若 ![]() ,
, ![]() ,求⊙O的面积.
,求⊙O的面积.
参考答案:
【答案】
(1)解:连接OD.
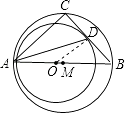
∵AB为直径,
∴∠ACB=90°,
∵OA=OD,
∴∠ODA=∠OAD,
∵AD平分∠CAB,
∴∠OAD=∠CAD,
∴∠ODA=∠CAD,
∴OD∥AC,
∴∠ODB=∠ACB=90°,
∴BD是⊙O的切线.
(2)解:∵ ![]() ,
,
∴AB=4AC,
∵BC2=AB2﹣AC2,
∴15AC2=80,
∴AC= ![]() ,
,
∴AB=4 ![]() .
.
设⊙O的半径为r,
∵OD∥AC,
∴△BOD∽△BAC,
∴ ![]()
∴  ,解得:r=
,解得:r= ![]()
∴πr2=π( ![]() )2=
)2= ![]() ,
,
∴⊙O的面积为 ![]() .
.
【解析】(1)连接OD,求出∠CAD=∠OAD=∠ADO,推出OD∥AC,推出OD⊥CB,根据切线判定推出即可;(2)根据勾股定理求出AC= ![]() ,AB=4
,AB=4 ![]() .设⊙O的半径为r,证△BOD∽△BAC,得出
.设⊙O的半径为r,证△BOD∽△BAC,得出 ![]() ,代入求出r即可.
,代入求出r即可.
【考点精析】解答此题的关键在于理解勾股定理的概念的相关知识,掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2,以及对切线的判定定理的理解,了解切线的判定方法:经过半径外端并且垂直于这条半径的直线是圆的切线.
-
科目: 来源: 题型:
查看答案和解析>>【题目】海上有一小岛,为了测量小岛两端A、B的距离,测量人员设计了一种测量方法,如图所示,已知B点是CD的中点,E是BA延长线上的一点,测得AE=8.3海里,DE=30海里,且DE⊥EC,cos∠D=
 .
. 
(1)求小岛两端A、B的距离;
(2)过点C作CF⊥AB交AB的延长线于点F,求sin∠BCF的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】我市某商场有甲、乙两种商品,甲种每件进价15元,售价20元;乙种每件进价35元,售价45元.
(1)若商家同时购进甲、乙两种商品100件,设甲商品购进x件,售完此两种商品总利润为y 元.写出y与x的函数关系式.
(2)该商家计划最多投入3000元用于购进此两种商品共100件,则至少要购进多少件甲种商品?若售完这些商品,商家可获得的最大利润是多少元?
(3)“五一”期间,商家对甲、乙两种商品进行表中的优惠活动,小王到该商场一次性付款324元购买此类商品,商家可获得的最小利润和最大利润各是多少?打折前一次性购物总金额
优惠措施
不超过400元
售价打九折
超过400元
售价打八折
-
科目: 来源: 题型:
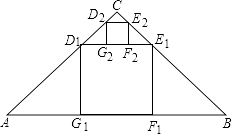
查看答案和解析>>【题目】如图,在Rt△ABC中,∠ACB=90°,AC=BC=2,在Rt△ABC内部作正方形D1E1F1G1 , 其中点D1 , E1分别在AC,BC边上,边F1G1在BC上,它的面积记作S1;按同样的方法在△CD1E1内部作正方形D2E2F2G2 , 它的面积记作S2 , S2= , …,照此规律作下去,正方形DnEnFnGn的面积Sn= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示在△ABC中,∠C=90°,AC=BC,AD平分∠CAB交BC于D,DE⊥BA于E,AB=6厘米,则△DEB的周长是_____厘米.

-
科目: 来源: 题型:
查看答案和解析>>【题目】解方程
(1)解方程组: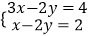
(2)已知关于x的一元二次方程x2+2x﹣m=1有实数根,求m的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】小明为班级联欢会设计了一个摸球游戏.游戏规则如下:在一个不透明的纸箱里装有红、黄、蓝三种颜色的小球,它们除颜色外完全相同,其中红球有2个,黄球有1个,蓝球有1个.游戏者先从纸箱里随机摸出一个球,记录颜色后放回,将小球摇匀,再随机摸出一个球,若两次摸到的球颜色相同,则游戏者可获得一份纪念品.请你利用树状图或列表法求游戏者获得纪念品的概率.
相关试题

