【题目】如图,正方形OABC的边长为6,点A、C分别在x轴,y轴的正半轴上,点D(2,0)在OA上,P是OB上一动点,则PA+PD的最小值为 . 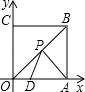
参考答案:
【答案】2 ![]()
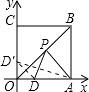
【解析】解:过D点作关于OB的对称点D′,连接D′A交OB于点P,由两点之间线段最短可知D′A即为PA+PD的最小值, ∵D(2,0),四边形OABC是正方形,
∴D′点的坐标为(0,2),A点坐标为(6,0),
∴D′A= ![]() =2
=2 ![]() ,即PA+PD的最小值为2
,即PA+PD的最小值为2 ![]() .
.
所以答案是2 ![]() .
.
【考点精析】关于本题考查的轴对称-最短路线问题,需要了解已知起点结点,求最短路径;与确定起点相反,已知终点结点,求最短路径;已知起点和终点,求两结点之间的最短路径;求图中所有最短路径才能得出正确答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校260名学生参加植树活动,要求每人植4~7棵,活动结束后随机抽查了20名学生每人的植树量,并分为四种类型,A:4棵;B:5棵;C:6棵;D:7棵.将各类的人数绘制成扇形图(如图1)和条形图(如图2),经确认扇形图是正确的,而条形图尚有一处错误.
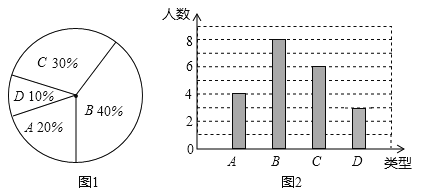
回答下列问题:
(1)写出条形图中存在的错误,并说明理由;
(2)写出这20名学生每人植树量的众数、中位数;
(3)在求这20名学生每人植树量的平均数时,小王是这样分析的:

① 小王的分析是从哪一步开始出现错误的?
② 请你帮他计算出正确的平均数,并估计这260名学生共植树多少棵.
-
科目: 来源: 题型:
查看答案和解析>>【题目】解方程:x2﹣3x=﹣2
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知双曲线
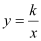 经过点D(6,1),点C是双曲线第三象限分支上的动点,过C作CA⊥x轴,过D作DB⊥y轴,垂足分别为A,B,连接AB,BC.
经过点D(6,1),点C是双曲线第三象限分支上的动点,过C作CA⊥x轴,过D作DB⊥y轴,垂足分别为A,B,连接AB,BC.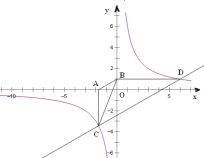
(1)求k的值;
(2)若△BCD的面积为12,求直线CD的解析式;
(3)判断AB与CD的位置关系,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,∠B=45°,∠C=30°,点D是BC上一点,连接AD,过点A作AG⊥AD,在AG上取点F,连接DF.延长DA至E,使AE=AF,连接EG,DG,且GE=DF.
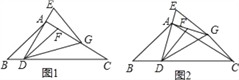
(1)若AB=2
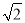 ,求BC的长;
,求BC的长;(2)如图1,当点G在AC上时,求证:BD=
 CG;
CG;(3)如图2,当点G在AC的垂直平分线上时,直接写出
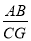 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】某学校去年在某商场购买甲、乙两种不同足球,购买甲种足球共花费2400元,购买乙种足球共花费1600元,购买甲种足球数量是购买乙种足球数量的2倍.且购买一个乙种足球比购买一个甲种足球多花20元.
(1)求购买一个甲种足球、一个乙种足球各需多少元;
(2)今年学校为编排“足球操”,决定再次购买甲、乙两种足球共50个.如果两种足球的单价没有改变,而此次购买甲、乙两种足球的总费用不超过3500元,那么这所学校最少可购买多少个甲种足球?
-
科目: 来源: 题型:
查看答案和解析>>【题目】平面上有6条直线,共有12个不同的交点,画出它们可能的位置关系(画三种图形).
相关试题

