【题目】如图,已知点E是ABCD中BC边的中点,若∠ABE=∠BAE=60°,BC=4,连接AE并延长交DC的延长线于点F. 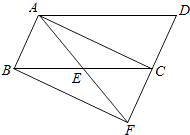
(1)连接AC,BF,求证:四边形ABFC为矩形;
(2)求四边形ABFC的周长和面积.
参考答案:
【答案】
(1)证明:∵四边形ABCD为平行四边形,
∴AB∥DC.
∴∠ABE=∠ECF.
又∵点E为BC的中点,∴BE=CE.
在△ABE和△FCE中, 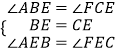
∴△ABE≌△FCE(ASA).
∴AB=CF.
又AB∥CF,
∴四边形ABFC为平行四边形.
∴AE=EF.
∵∠ABE=∠BAE=60°,
∴AE=BE,即AF=BC
∴四边形ABFC为矩形
(2)解:∵在矩形ABFC中,∠ABE=∠BAE=60°,BC=4
∴△ABE是等边三角形,
∴AB=BE=2.
∴AC= ![]() =2
=2 ![]() .
.
∴四边形ABFC的周长=2(AB+AC)=2(2+2)=4+4.
S四边形ABFC=2 ![]() ×2=4
×2=4 ![]()
【解析】(1)利用ASA可得出三角形ABE与三角形FCE全等;进而得出AB=FC,即可得出四边形ABFC是平行四边形,再由直角三角形的判定方法得出△BFC是直角三角形,即可得出平行四边形ABFC是矩形.(2)由等边三角形的性质得出∠AFC=60°,AF=DF=4,得出CF=CD=2,由矩形的性质得出∠ACF=90°,得出AC= ![]() CF=2
CF=2 ![]() ,即可得出四边形ABFC的面积=ACCF=4
,即可得出四边形ABFC的面积=ACCF=4 ![]() .
.
【考点精析】解答此题的关键在于理解平行四边形的性质的相关知识,掌握平行四边形的对边相等且平行;平行四边形的对角相等,邻角互补;平行四边形的对角线互相平分.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(在矩形ABCD中,AB=4,BC=8,经过对角线交点O的直线EF绕点O旋转,分别交AD、BC于点E、F,连接AF、CE.
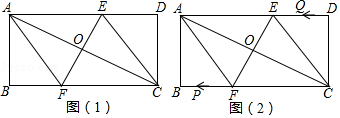
(1)如图(1),依据下列条件在普通四边形、梯形、普通平行四边形、矩菱形或正方形中选择填空:旋转过程中四边形AFCE始终为;
当点E为AD的中点时四边形AFCE为;
当EF⊥AC时四边形AFCE为;
(2)如图(1),当EF⊥AC时,求AF的长;
(3)如图(2),在(2)的基础上,若动点P从A点出发,沿A→F→B→A运动一周停止,速度为每秒5厘米;同时点Q从C点出发,沿C→D→E→C运动一周停止,速度为每秒4厘米,在P、Q运动过程中,第几秒时,四边形APCQ是平行四边形? -
科目: 来源: 题型:
查看答案和解析>>【题目】下列方程中,有两个不相等的实数根的是 ( )
A. x2+2=0B. (x﹣1)2=0C. x2+2x﹣1=0D. x2+x+5=0
-
科目: 来源: 题型:
查看答案和解析>>【题目】《九章算术》中有注:“今两算得失相反,要令正负以名之。”意思是:“今有两数若其意义相反,则分别叫做正数和负数。”如果水位升高5米记为+5米,那么水位下降3米应记为( )
A. -5米 B. +5米 C. -2米 D. -3米
-
科目: 来源: 题型:
查看答案和解析>>【题目】2018年足球世界杯期间,俄罗斯总收入约为87亿美元,其中87亿用科学记数法表示为( )
A. 8.7×108 B. 8.7×109 C. 8.7×1010 D. 0.87×1010
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AD⊥BC,垂足为D,∠B=60°,∠C=45°.
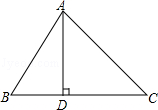
(1)求∠BAC的度数.
(2)若AD=2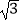 ,求AC和AB的长.
,求AC和AB的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】小明在课外学习时遇到这样一个问题:
定义:如果二次函数
 是常数与
是常数与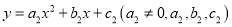 是常数)满足
是常数)满足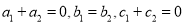 ,则称这两个函数互为“旋转函数”.
,则称这两个函数互为“旋转函数”.求函数
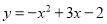 的 “旋转函数”.
的 “旋转函数”.小明是这样思考的:由
 函数可知a1=-1,b1=3,c1=-3,根据a1+a2=0,b1=b2,c1+c2=0求出a2,b2,c2,就能确定这个函数的“旋转函数”.
函数可知a1=-1,b1=3,c1=-3,根据a1+a2=0,b1=b2,c1+c2=0求出a2,b2,c2,就能确定这个函数的“旋转函数”.请参考小明的方法解决下面的问题:
(1)写出函数
 的“旋转函数”;
的“旋转函数”;(2)若函数
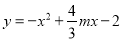 与
与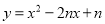 互为“旋转函数”,求(m+n)2017的值;
互为“旋转函数”,求(m+n)2017的值;(3)已知函数
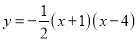 的图象与
的图象与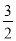 轴交于A、B两点,与y轴交于点C,点A、B、C关于原点的对称点分别是A1、B1、C1,试证明经过点A1、B1、C1的二次函数与函数
轴交于A、B两点,与y轴交于点C,点A、B、C关于原点的对称点分别是A1、B1、C1,试证明经过点A1、B1、C1的二次函数与函数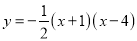 互为“旋转函数”.
互为“旋转函数”.
相关试题

