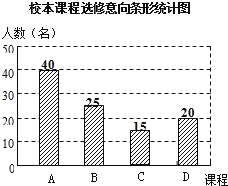
【题目】某学校计划开设A、B、C、D四门校本课程供学生选修,规定每个学生必须并且只能选修其中一门,为了了解学生的选修意向,现随机抽取了部分学生进行调查,并将调查结果绘制成如下所示的两个不完整统计图表.
校本课程选修意向统计表
选修课程 | 所占百分比 |
A | a% |
B | 25% |
C | b% |
D | 20% |
请根据图表信息,解答下列问题:
(1)参与调查的学生有 名;
(2)在统计表中,a= ,b= ,请你补全条形统计图;
(3)若该校共有2000名学生,请你估算该校有多少名学生选修A课程?

参考答案:
【答案】(1)100;(2)40,15,图见试题及解析;(3)该校有800名学生选修A课程.
【解析】
试题分析:(1)根据条形统计图和表格可知选B的有25人占调查学生的25%,从而可以求得参与调查的学生数;
(2)根据调查的学生数可以求得a、b的值,以及选D的学生数,从而可以将条形统计图补充完整;
(3)根据表格总选A的学生所占的百分比,可以估算该校有多少名学生选修A课程.
试题解析:(1)根据条形统计图和表格可知,选B的有25人占调查学生的25%,
∴参与调查的学生有:25÷25%=100(名),故答案为:100;
(2)由(1)和表格可得,a%=40÷100×100%=40%,b%=15÷100×100%=15%,
故答案为:40,15,
选D的学生有:100×20%=20(名)
补全条形统计图如右图所示,
(3)由题意可得,
40%×2000=800(名)
即该校有800名学生选修A课程.
-
科目: 来源: 题型:
查看答案和解析>>【题目】解不等式1﹣
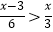 ,并把解集在数轴上表示出来.
,并把解集在数轴上表示出来. 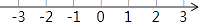
-
科目: 来源: 题型:
查看答案和解析>>【题目】请写出一个多项式(最多三项),使它能先“提公因式”,再“运用公式”来分解因式.你编写的多项式是:_______________,分解因式的结果是________________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】将三张质地相同并分别标有数字1、2、3的卡片,背面朝上放在桌面上,洗匀后,甲同学从中随机抽取一张卡片.
(1)甲同学抽到卡片上的数恰好是方程x2﹣4x+3=0的根的概率为 ;
(2)甲乙两人约定:甲先随机抽取一张卡片后,背面朝上放回桌面洗匀,然后乙再随机抽取一张卡片,若两人所抽取卡片上的数字恰好是方程x2﹣4x+3=0的两个根,则甲获胜;否则乙获胜.请你通过列表或画树状图的方法,说明这个游戏是否公平?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知a、b、c为△ABC的三边,且满足a2c2﹣b2c2=a4﹣b4,则△ABC是( )
A.直角三角形B.等腰三角形
C.等腰三角形或直角三角形D.等腰直角三角形
-
科目: 来源: 题型:
查看答案和解析>>【题目】解不等式
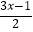 ﹣1≤
﹣1≤ 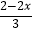 ,并把解集在数轴上表示出来.
,并把解集在数轴上表示出来. -
科目: 来源: 题型:
查看答案和解析>>【题目】在某个样本的频数分布直方图中,第二组的频数为20,占抽样数据的40%,则样本容量为________.
相关试题

