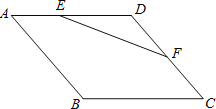
【题目】如图,菱形ABCD的边长为4,∠BAD=60°,点E是AD上一动点(不与A、D重合),点F是CD上一动点,且AE+CF=4,则△DEF面积的最大值为__________
参考答案:
【答案】![]()
【解析】首先过点F作FG⊥AD,交AD的延长线于点G,由菱形ABCD的边长为4,∠BAD=60°,即可求得AD=CD=4,∠FDG=60°,然后设AE=x,即可得S△DEF=![]() DEFG=﹣
DEFG=﹣![]() (x﹣2)2+
(x﹣2)2+![]() ,然后根据二次函数的性质,即可求得答案.
,然后根据二次函数的性质,即可求得答案.
过点F作FG⊥AD,交AD的延长线于点G.
∵菱形ABCD边长为4,∠BAD=60°,∴AD=CD=4,∠ADB=180°﹣∠BAD=120°,∴∠FDG=180°﹣∠ADB=60°,设AE=x.
∵AE+CF=4,∴CF=4﹣x;
∴DE=AD﹣AE=4﹣x,DF=CD﹣CF=4﹣(4﹣x)=x.在Rt△DFG中,FG=DFsin∠GDF=![]() x,∴S△DEF=
x,∴S△DEF=![]() DEFG=
DEFG=![]() ×(4﹣x)×
×(4﹣x)×![]() x=﹣
x=﹣![]() x2+
x2+![]() x=﹣
x=﹣![]() (x2﹣4x)=﹣
(x2﹣4x)=﹣![]() (x﹣2)2+
(x﹣2)2+![]() ,∴当x=2时,△DEF面积的最大,最大值为
,∴当x=2时,△DEF面积的最大,最大值为![]() .
.
故答案为:![]() .
.
-
科目: 来源: 题型:
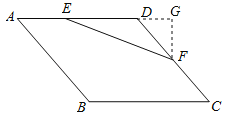
查看答案和解析>>【题目】如图,点A是双曲线y=
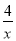 在第一象限上的一动点,连接AO并延长交另一分支于点B,以AB为斜边作等腰Rt△ABC,点C在第二象限,随着点A的运动,点C的位置也不断的变化,但始终在一函数图象上运动,则这个函数的解析式为 .
在第一象限上的一动点,连接AO并延长交另一分支于点B,以AB为斜边作等腰Rt△ABC,点C在第二象限,随着点A的运动,点C的位置也不断的变化,但始终在一函数图象上运动,则这个函数的解析式为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】学生刘明,对某校六1班上学期期末的数学成绩(成绩取整数,满分为100分)作了统计,发现这个班每个人的成绩各不相同,并据此绘制成如下频数分布表和频数分布直方图.请你根据图表提供的信息,解答下列问题:
分组
49.5~59.5
59.5~69.5
69.5~79.5
79.5~89.5
89.5~100.5
合计
频数
2
8
20
a
4
c
频率
0.04
b
0.40
0.32
0.08
1
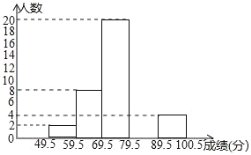
(1)频数、频率分布表中a=____,b=_____,c=_____;
(2)补全频数分布直方图;
(3)如果要画该班上学期期末数学成绩的扇形统计图,那么分数在69.5﹣79.5之间的扇形圆心角的度数是_______.
(4)张亮同学成绩为79分,他说:“我们班上比我成绩高的人还有
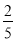 ,我要继续努力.”他的说法正确吗?请说明理由.
,我要继续努力.”他的说法正确吗?请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】P是三角形
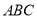 内一点,射线PD//AC ,射线PB//AB .
内一点,射线PD//AC ,射线PB//AB .(1)当点D,E分别在AB,BC 上时,
①补全图1:
②猜想
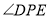 与
与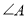 的数量关系,并证明;,
的数量关系,并证明;,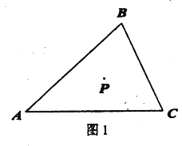
(2)当点
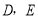 都在线段
都在线段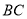 上时,请先画出图形,想一想你在(1)中所得结论是否仍然成立?若成立,请证明;若不成立,请说明理由
上时,请先画出图形,想一想你在(1)中所得结论是否仍然成立?若成立,请证明;若不成立,请说明理由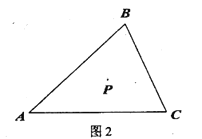
-
科目: 来源: 题型:
查看答案和解析>>【题目】(11·漳州)(满分8分)漳州市某中学对全校学生进行文明礼仪知识测试,为了解测试结果,随机抽取部分学生的成绩进行分析,将成绩分为三个等级:不合格、一般、优秀,并绘制成如下两幅统计图(不完整).请你根据图中所给的信息解答下列问题:

(1)请将以上两幅统计图补充完整;
(2)若“一般”和“优秀”均被视为达标成绩,则该校被抽取的学生中有_ ▲ 人达标;
(3)若该校学生有1200人,请你估计此次测试中,全校达标的学生有多少人?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直角坐标系中,△ABC的顶点都在网格点上,其中,C点坐标为(1,2),
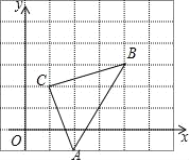
(1)写出点A、B的坐标:A( , )、B( , )
(2)将△ABC先向左平移1个单位长度,再向上平移2个单位长度,得到△A′B′C′,画出△A′B′C′
(3)写出三个顶点坐标A′( 、 )、B′( 、 )、C′ 、 )
(4)求△ABC的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】股民王晓宇上周五在股市以收盘价(股市收市时的价格)每股24元购买进某公司股票1000股,周六、周日股市不交易,在接下来的一周交易日内,王晓宇记下该股每日收盘价格相比前一天的涨跌情况如下表:(单位:元)

(1)星期三收盘时,每股是多少元?
(2)已知小明父亲买进股票时付了1.5‰的手续费,卖出时需付成交额的1.5‰的手续费和1‰的交易税,如果他在周五收盘前将全部股票卖出,他的收益情况如何?
相关试题

