【题目】如图,在平面直角坐标系xOy中,已知正比例函数y=![]() x的图象与反比例函数y=
x的图象与反比例函数y=![]() 的图象交于A(a,-2),B两点.
的图象交于A(a,-2),B两点.
(1)求反比例函数的表达式和点B的坐标;
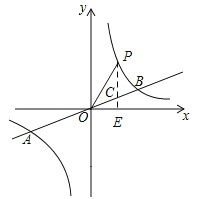
(2)P是第一象限内反比例函数图象上一点,过点P作y轴的平行线,交直线AB于点C,连接PO,若△POC的面积为3,求点P的坐标.

参考答案:
【答案】(1)y=![]() ,B(4,2);(2)P
,B(4,2);(2)P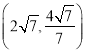 或(2,4).
或(2,4).
【解析】试题分析:(1)把A(a,﹣2)代入![]() ,可得A(﹣4,﹣2),把A(﹣4,﹣2)代入
,可得A(﹣4,﹣2),把A(﹣4,﹣2)代入![]() ,可得反比例函数的表达式为
,可得反比例函数的表达式为![]() ,再根据点B与点A关于原点对称,即可得到B的坐标;
,再根据点B与点A关于原点对称,即可得到B的坐标;
(2)过P作PE⊥x轴于E,交AB于C,先设P(m, ![]() ),则C(m,
),则C(m, ![]() m),根据△POC的面积为3,可得方程
m),根据△POC的面积为3,可得方程![]() =3,求得m的值,即可得到点P的坐标.
=3,求得m的值,即可得到点P的坐标.
(1)把A(a,﹣2)代入![]() ,可得a=﹣4,∴A(﹣4,﹣2),把A(﹣4,﹣2)代入
,可得a=﹣4,∴A(﹣4,﹣2),把A(﹣4,﹣2)代入![]() ,可得k=8,∴反比例函数的表达式为
,可得k=8,∴反比例函数的表达式为![]() ,∵点B与点A关于原点对称,∴B(4,2);
,∵点B与点A关于原点对称,∴B(4,2);
(2)如图所示,过P作PE⊥x轴于E,交AB于C,设P(m, ![]() ),则C(m,
),则C(m, ![]() m),∵△POC的面积为3,∴
m),∵△POC的面积为3,∴![]() =3,解得m=
=3,解得m=![]() 或2,∴P(
或2,∴P(![]() ,
, ![]() )或(2,4).
)或(2,4).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系
 中,函数
中,函数 的图象与直线
的图象与直线 交于点A(3,m).
交于点A(3,m).(1)求k、m的值;
(2)已知点P(n,n)(n>0),过点P作平行于
 轴的直线,交直线y=x-2于点M,过点P作平行于y轴的直线,交函数
轴的直线,交直线y=x-2于点M,过点P作平行于y轴的直线,交函数 的图象于点N.
的图象于点N.①当n=1时,判断线段PM与PN的数量关系,并说明理由;
②若PN≥PM,结合函数的图象,直接写出n的取值范围.

-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,高AD和BE所在的直线交于点H,且BH=AC,则∠ABC等于( )
A. 45° B. 120° C. 45°或135° D. 45°或120°
-
科目: 来源: 题型:
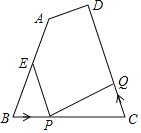
查看答案和解析>>【题目】如图,已知四边形ABCD中,AB=12厘米,BC=8厘米,CD=14厘米,∠B=∠C,点E为线段AB的中点.如果点P在线段BC上以3厘米秒的速度由B点向C点运动,同时,点Q在线段CD上由C点向D点运动.当点Q的运动速度为_____厘米/秒时,能够使△BPE与以C、P、Q三点所构成的三角形全等.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,一次函数y=﹣ax+b的图象与反比例函数
 的图象相交于点A(﹣4,﹣2),B(m,4),与y轴相交于点C.
的图象相交于点A(﹣4,﹣2),B(m,4),与y轴相交于点C.(1)求反比例函数和一次函数的表达式;
(2)求点C的坐标及△AOB的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点A(m,m+1),B(m+1,2m-3)都在反比例函数
 的图象上.
的图象上.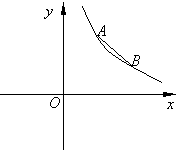
(1)求m,k的值;
(2)如果M为x轴上一点,N为y轴上一点, 以点A,B,M,N为顶点的四边形是平行四边形,试求直线MN的函数表达式.
-
科目: 来源: 题型:
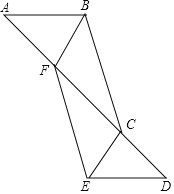
查看答案和解析>>【题目】如图,在△ABC和△DEF中,AB∥DE,点A,F,C,D在同一直线上,AF=CD,∠AFE=∠BCD.
试说明:
(1)△ABC≌△DEF;
(2)BF∥EC.
相关试题

