【题目】如图,在△ABC和△DEF中,AB∥DE,点A,F,C,D在同一直线上,AF=CD,∠AFE=∠BCD.
试说明:
(1)△ABC≌△DEF;
(2)BF∥EC.
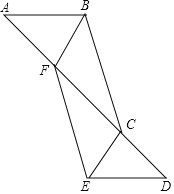
参考答案:
【答案】(1)见解析;(2)见解析.
【解析】
(1)由平行线的性质,根据全等三角形的判定(ASA)即可得到答案;
(2)根据全等三角形的性质和判定(SAS)进行证明即可得到答案.
(1)∵AB∥DE,∴∠A=∠D
∵AF=CD,∴AF+FC=CD+FC 即 AC=DF
∵∠AFE=∠BCD,∴∠DFE=∠ACB
在△ABC和△DEF中,
∴△ABC≌△DEF (ASA)
(2)∵△ABC≌△DEF
∴BC=EF
在△BCF和△EFC中,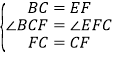
∴△BCF≌△EFC (SAS)
∴∠BFC=∠ECF
∴BF∥EC
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校七年级有400名学生,其中2004年出生的有8人,2005年出生的有292人,2006年出生的有75人,其余的为2007年出生.
(1)该年级至少有两人同月同日生,这是一个 事件(填“必然”、“不可能”或“随机”);
(2)从这400名学生中随机选一人,选到2007年出生的概率是多少?
-
科目: 来源: 题型:
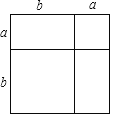
查看答案和解析>>【题目】如图所示的大正方形是由两个小正方形和两个长方形组成.
(1)通过两种不同的方法计算大正方形的面积,可以得到一个数学等式;
(2)利用(1)中得到的结论,解决下面的问题:若a+b=2,ab=﹣3,
求:①a2+b2;
②a4+b4.
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲骑电动车从A地到B地,乙骑自行车从B地到A地,两人同时出发,设乙骑自行车的时间为t(h),两人之间的距离为s(km),图中的折线表示s和t之间的关系,根据图象回答下列问题.
(1)A、B两地之间的距离为 km;
(2)求甲出发多长时间与乙相遇?

-
科目: 来源: 题型:
查看答案和解析>>【题目】问题背景:某数学兴趣小组把两个等腰直角三角形的直角顶点重合,发现了一些有趣的结论.
结论一:
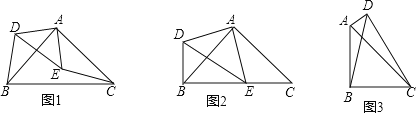
(1)如图1,在△ABC、△ADE中,∠BAC=∠DAE=90°,AB=AC,AD=AE,连接BD,CE,试说明△ADB≌△AEC;
结论二:
(2)如图2,在(1)的条件下,若点E在BC边上,试说明DB⊥BC;
应用:
(3)如图3,在四边形ABCD中,∠ABC=∠ADC=90°,AB=CB,∠BAD+∠BCD=180°,连接BD,BD=7cm,求四边形ABCD的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】以下说法合理的是( )
A. 小明在10次抛图钉的试验中发现3次钉尖朝上,由此他说钉尖朝上的概率是30%
B. 抛掷一枚普通的正六面体骰子,出现6的概率是
 的意思是每6次就有1次掷得6
的意思是每6次就有1次掷得6C. 某彩票的中奖机会是2%,那么如果买100张彩票一定会有2张中奖。
D. 在一次课堂进行的试验中,甲、乙两组同学估计硬币落地后,正面朝上的概率分别为0.48和0.51。
-
科目: 来源: 题型:
查看答案和解析>>【题目】某公司生产A种产品,它的成本是6元/件,售价是8元/件,年销售量为5万件.为了获得更好的效益,公司准备拿出一定的资金做广告,根据经验,每年投入的广告费是x万元,产品的年销售量将是原销售量的y倍,且y与x之间满足我们学过的二种函数(即一次函数和二次函数)关系中的一种,它们的关系如下表:
x(万元)
0
0.5
1
1.5
2
…
y
1
1.275
1.5
1.675
1.8
…
(1)求y与x的函数关系式(不要求写出自变量的取值范围)
(2)如果把利润看作是销售总额减去成本费用和广告费用,试求出年利润W(万元)与广告费用x(万元)的函数关系式,并计算每年投入的广告费是多少万元时所获得的利润最大?
(3)如果公司希望年利润W(万元)不低于14万元,请你帮公司确定广告费的范围.
相关试题

