【题目】如图,AB为⊙O的直径,AC、DC为弦,∠ACD=60°,P为AB延长线上的点,∠APD=30°.
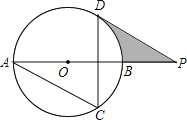
(1)求证:DP是⊙O的切线;
(2)若⊙O的半径为3cm,求图中阴影部分的面积.
参考答案:
【答案】(1)见解析;(2)(![]()
![]() ﹣
﹣![]() π)cm2
π)cm2
【解析】
试题分析:(1)连接OD,求出∠AOD,求出∠DOB,求出∠ODP,根据切线判定推出即可;
(2)求出OP、DP长,分别求出扇形DOB和三角形ODP面积,即可求出答案.
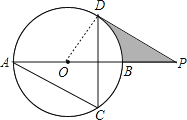
【解答】(1)证明:连接OD,
∵∠ACD=60°,
∴由圆周角定理得:∠AOD=2∠ACD=120°,
∴∠DOP=180°﹣120°=60°,
∵∠APD=30°,
∴∠ODP=180°﹣30°﹣60°=90°,
∴OD⊥DP,
∵OD为半径,
∴DP是⊙O切线;
(2)解:∵∠P=30°,∠ODP=90°,OD=3cm,
∴OP=6cm,由勾股定理得:DP=3![]() cm,
cm,
∴图中阴影部分的面积S=S△ODP﹣S扇形DOB=![]() ×3×3
×3×3![]() ﹣
﹣![]() =(
=(![]()
![]() ﹣
﹣![]() π)cm2
π)cm2
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一抛物线经过点A(﹣2,0),点B(0,4)和点C(4,0),该抛物线的顶点为D.
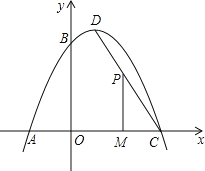
(1)求该抛物线的函数关系式及顶点D坐标.
(2)如图,若P为线段CD上的一个动点,过点P作PM⊥x轴于点M,求四边形PMAB的面积的最大值和此时点P的坐标.
(3)过抛物线顶点D,作DE⊥x轴于E点,F(m,0)是x轴上一动点,若以BF为直径的圆与线段DE有公共点,求m的取值范围.
-
科目: 来源: 题型:
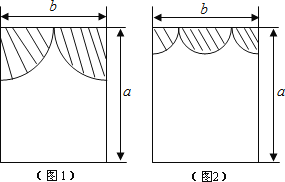
查看答案和解析>>【题目】小亮房间窗户的窗帘如图1所示,它是由两个四分之一圆组成(半径相同)
(1)用代数式表示窗户能射进阳光的面积是 .(结果保留π)
(2)当
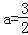 ,b=1时,求窗户能射进阳光的面积是多少?(取π≈3)
,b=1时,求窗户能射进阳光的面积是多少?(取π≈3)(3)小亮又设计了如图2的窗帘(由一个半圆和两个四分之一圆组成,半径相同),请你帮他算一算此时窗户能射进阳光的面积是否更大?如果更大,那么大多少?(结果保留π)
-
科目: 来源: 题型:
查看答案和解析>>【题目】某食品公司产销一种食品,已知每月的生产成本y1与产量x之间是一次函数关系,函数y1与自变量z(kg)的部分对应值如下表:
x(单位:kg)
10
20
30
y1(单位:/元)
3030
3060
3090
(1)求y1与x之间的函数关系式;
(2)经过试销发现,这种食品每月的销售收入y2(元)与销量x(kg)之间满足如图所示的函数关系
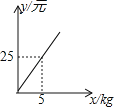
①y2与x之间的函数关系式为 ;
②假设该公司每月生产的该种食品均能全部售出,那么该公司每月至少要生产该种食品多少kg,才不会亏损?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形ABCD中,E为BC上一点,DF⊥AE于F.

(1)△ABE与△ADF相似吗?请说明理由.
(2)若AB=6,AD=12,BE=8,求DF的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知a2﹣a﹣1=0,则a3﹣a2﹣a+2016=__.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:26=a2=4b,则a+b= ______ .
相关试题

