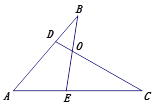
【题目】如图,点D在AB上,点E在AC上,BE、CD相交于点O.
(1)若∠A=50°,∠BOD=70°,∠C=30°,求∠B的度数;
(2)试猜想∠BOC与∠A+∠B+∠C之间的关系,并证明你猜想的正确性.
参考答案:
【答案】(1)30°;(2)∠BOC=∠A+∠B+∠C,理由见解析.
【解析】
(1)利用三角形外角的性质和三角形内角和定理即可求得∠B的度数;(2)用三角形外角和定理求出∠BOC,∠BEC的两角之和,最后得出结论.
解:(1)∵∠A=50°,∠C=30°,∴∠BDO=80°;∵∠BOD=70°,∴∠B=30°;
(2)∠BOC=∠A+∠B+∠C.
理由:∵∠BOC=∠BEC +∠C,∠BEC=∠A+∠B,
∴∠BOC=∠A+∠B+∠C.
-
科目: 来源: 题型:
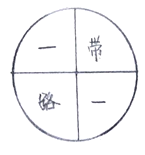
查看答案和解析>>【题目】“一带一路”是指“丝绸之路经济带”和“21世纪海上丝绸之路”的简称.数学兴趣小组设计了一个可以自由转动的均匀转盘,转盘被分成相等的4份,且每份分别标有“一”、“带”、“一”、“路”的字.任意转动转盘,转盘停止后,指针都会指向其中的一个字(如果指针恰好停在等分线上,那么重新转一次,直到指针指向转盘中四等份中的某一份为止)
(1)转动转盘一次,求指针恰好指到“一”字的概率;
(2)连续转动转盘两次,请用列表或者画树状图的方法求指针两次都指向“一”字的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,已知直线PQ∥MN,点A在直线PQ上,点C、D在直线MN上,连接AC、AD,∠PAC=50°,∠ADC=30°,AE平分∠PAD,CE平分∠ACD,AE与CE相交于点E.



(1)若将图1中的线段AD沿MN向右平移到A1D1如图2所示位置,此时A1E平分∠AA1D1,CE平分∠ACD1,A1E与CE相交于E,∠PAC=50°,∠A1D1C=30°,求∠A1EC的度数.
(2)若将图1中的线段AD沿MN向左平移到A1D1如图3所示位置,其他条件与(1)相同,求此时∠A1EC的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】我们知道,任意一个有理数与无理数的和为无理数,任意一个不为零的有理数与一个无理数的积为无理数,而零与无理数的积为零.由此可得:如果mx+n=0,其中m、n为有理数,x为无理数,那么m=0且n=0.
(1)如果
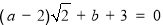 ,其中a、b为有理数,那么a= ,b= .
,其中a、b为有理数,那么a= ,b= .(2)如果
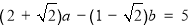 ,其中a、b为有理数,求a+2b的值.
,其中a、b为有理数,求a+2b的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,线段AB、CD相交于点O,连结AD、CB,我们把形如图1的图形称之为“8字形”.如图2,在图1的条件下,∠DAB和∠BCD的平分线AP和CP相交于点P,并且与CD、AB分别相交于点M、N.试解答下列问题:

(1)在图1中,请直接写出∠A、∠B、∠C、∠D之间的数量关系;
(2)仔细观察,在图2中“8字形”有多少个;
(3)图2中,当∠D=50°,∠B=40°时,求∠P的度数.
-
科目: 来源: 题型:
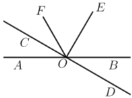
查看答案和解析>>【题目】如图,直线
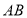 、
、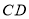 相交于点
相交于点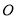 ,
,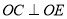 ,
,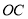 平分
平分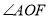 ,
,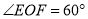 .
.
(1)求
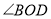 的大小,根据下列解答填空(理由或数学式)
的大小,根据下列解答填空(理由或数学式)解:∵
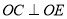 (已知),
(已知),∴
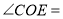 ______°,
______°,∵
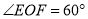 ,
,∴
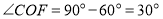 .
.∵
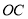 平分
平分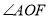 (已知),
(已知),∴
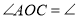 ______
______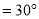 .
.∵
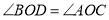 (______),
(______),∴
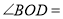 ______°.
______°.(2)直接写出图中所有与
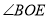 互余的角.
互余的角. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AB=AC,BE=CE,下面四个结论:①BP=CP;②AD⊥BC;③AE平分∠BAC;④∠PBC=∠PCB.其中正确的结论个数有( )个.
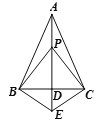
A. 1B. 2C. 3D. 4
相关试题

