搜索
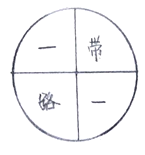
【题目】“一带一路”是指“丝绸之路经济带”和“21世纪海上丝绸之路”的简称.数学兴趣小组设计了一个可以自由转动的均匀转盘，转盘被分成相等的4份，且每份分别标有“一”、“带”、“一”、“路”的字.任意转动转盘，转盘停止后，指针都会指向其中的一个字（如果指针恰好停在等分线上，那么重新转一次，直到指针指向转盘中四等份中的某一份为止）
（1）转动转盘一次，求指针恰好指到“一”字的概率；
（2）连续转动转盘两次，请用列表或者画树状图的方法求指针两次都指向“一”字的概率.
参考答案：
【答案】（1）
；（2）
.
【解析】（1）列举出符合题意的各种情况的个数，再根据概率公式解答即可；
（2）列表或画树状图求出所有等可能的结果，找出两次都指向“一”的结果数，即可求解.
（1）由题意知共有四种情况，指到“一”字的情况有两种，
故指到“一”字的概率为
.
（2）列表如下：
一 | 带 | 一 | 路 | |
一 | 一、一 | 一、带 | 一、一 | 一、路 |
带 | 带、一 | 带、带 | 带、一 | 带、路 |
一 | 一、一 | 一、带 | 一、一 | 一、路 |
路 | 路、一 | 路、带 | 路、一 | 路、路 |
由表知共有16种结果，两次都指向“一”的结果有四种，故P（两次都指向“一”）=
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，
，
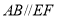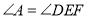.在下列解答中，填空（理由或数学式）：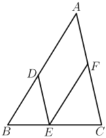
解：∵
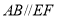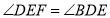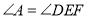（已知），∴
（______），∵
（已知），∴∠______=∠______（等量代换），
∴
______（______），∴
（______）. -
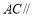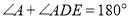科目： 来源： 题型：
查看答案和解析>>【题目】（1）已知：如图1，在△ABC中，∠ABC的平分线与∠ACB的平分线交于点O，求证：∠BOC=90°+
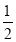∠A；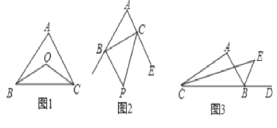
（2）如图2，在△ABC中，BP，CP分别是△ABC的外角∠DBC和∠ECB的平分线，试探究∠BPC与∠A的关系．
（3）如图3，在△ABC中，CE平分∠ACB，BE是△ABC的外角∠ABD的平分线，试探究∠BEC与∠A的关系．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在8×8的正方形网格中，每个小正方形的顶点称为格点，点A、B、C均在格点上，按下述要求画图并标注相关字母．
（1）画线段AB，画射线BC，画直线AC；
（2）过点B画线段BD⊥AC，垂足为点D；
（3）取线段AB的中点E，过点E画BD的平行线，交AC于点F．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图1，已知直线PQ∥MN，点A在直线PQ上，点C、D在直线MN上，连接AC、AD，∠PAC=50°，∠ADC=30°，AE平分∠PAD，CE平分∠ACD，AE与CE相交于点E.
（1）若将图1中的线段AD沿MN向右平移到A1D1如图2所示位置，此时A1E平分∠AA1D1，CE平分∠ACD1，A1E与CE相交于E，∠PAC=50°，∠A1D1C=30°，求∠A1EC的度数.
（2）若将图1中的线段AD沿MN向左平移到A1D1如图3所示位置，其他条件与（1）相同，求此时∠A1EC的度数.
-
科目： 来源： 题型：
查看答案和解析>>【题目】我们知道，任意一个有理数与无理数的和为无理数，任意一个不为零的有理数与一个无理数的积为无理数，而零与无理数的积为零.由此可得：如果mx+n=0，其中m、n为有理数，x为无理数，那么m=0且n=0.
（1）如果
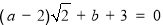，其中a、b为有理数，那么a= ，b= .（2）如果
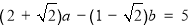，其中a、b为有理数，求a+2b的值. -
科目： 来源： 题型：
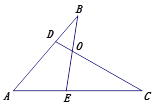
查看答案和解析>>【题目】如图，点D在AB上，点E在AC上，BE、CD相交于点O.
（1）若∠A=50°，∠BOD=70°，∠C=30°，求∠B的度数；
（2）试猜想∠BOC与∠A+∠B+∠C之间的关系，并证明你猜想的正确性.
相关试题
