【题目】在平面直角坐标系中,抛物线过原点O,且与![]() 轴交于另一点
轴交于另一点![]() ,其顶点为
,其顶点为![]() .孔明同学用一把宽为
.孔明同学用一把宽为![]() 带刻度的矩形直尺对抛物线进行如下测量:
带刻度的矩形直尺对抛物线进行如下测量:
① 量得![]() ;② 把直尺的左边与抛物线的对称轴重合,使得直尺左下端点与抛物线的顶点重合(如图1),测得抛物线与直尺右边的交点
;② 把直尺的左边与抛物线的对称轴重合,使得直尺左下端点与抛物线的顶点重合(如图1),测得抛物线与直尺右边的交点![]() 的刻度读数为
的刻度读数为![]() .
.
请完成下列问题:
(1)写出抛物线的对称轴;(2)求抛物线的解析式;(3)将图中的直尺(足够长)沿水平方向向右平移到点![]() 的右边(如图2),直尺的两边交
的右边(如图2),直尺的两边交![]() 轴于点
轴于点![]() 、
、![]() ,交抛物线于点
,交抛物线于点![]() 、
、![]() .求证:
.求证: ![]() .
.
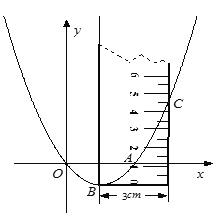
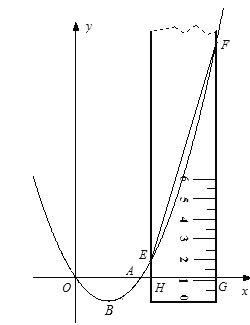
图1 图2
参考答案:
【答案】(1)![]() (2)
(2)![]() (3)
(3)![]()
【解析】试题分析:(1)由于O、A关于抛物线对称轴对称,且OA=3cm,由此可求得抛物线的对称轴为x=![]() .
.
(2)根据O、A的坐标,可将抛物线解析式设为交点式,在(1)题求得了抛物线的对称轴,即可得到B、C的横坐标,分别代入抛物线的解析式中,表示出它们的纵坐标,根据C、B的纵坐标差为4.5即可列方程求出待定系数的值,从而确定抛物线的解析式.
(3)可设出E点的横坐标,进而根据直尺的宽度得到F点的横坐标,根据(2)题所得抛物线,即可表示出两点的纵坐标,利用梯形的面积公式,可求出梯形EFGH的面积表达式,然后同![]() (EF2-9)进行比较即可.
(EF2-9)进行比较即可.
试题解析:(1)![]()
(2)设抛物线的解析式为: ![]() ,当
,当![]() 时,
时, ![]() ,即
,即![]() ;当
;当![]() 时,
时, ![]() ,即
,即![]() ,依题意得:
,依题意得: ![]() ,解得:
,解得: ![]() .
.
∴抛物线的解析式为: ![]() .
.
(3)过点![]() 作
作![]() ,垂足为
,垂足为![]() ,设
,设![]() ,
, ![]() ,得:
,得: ![]() ①
①
![]() ②
②
又![]() ,得
,得 ,分别代入①、②得:
,分别代入①、②得: ![]() ,
, ![]()
∴![]() 得:
得: ![]()
又![]() ∴
∴![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AD为△ABC的中线,BE为三角形ABD中线.
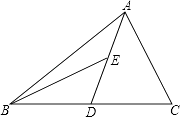
(1)在△BED中作BD边上的高EF;
(2)若△ABC的面积为40,BD=5,求EF的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】﹣a的相反数是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】135万用科学记数法可表示为_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线y=mx与双曲线y=
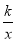 相交于A、B两点,A点的坐标为(1,2)
相交于A、B两点,A点的坐标为(1,2)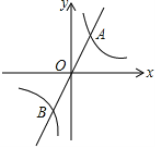
(1)求反比例函数的表达式;
(2)根据图象直接写出当mx>
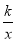 时,x的取值范围;
时,x的取值范围;(3)计算线段AB的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,高速公路BC(公路视为直线)的最高限速为120
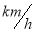 ,在该公路正上方离地面20
,在该公路正上方离地面20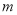 的点A处设置了一个测速仪,已知在点A测得点B的俯角为45°,点C的俯角为30°,测速仪监测到一辆汽车从点B匀速行驶到点C所用的时间是1.5
的点A处设置了一个测速仪,已知在点A测得点B的俯角为45°,点C的俯角为30°,测速仪监测到一辆汽车从点B匀速行驶到点C所用的时间是1.5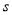 ,试通过计算,判决该汽车在这段限速路上是否超速.(参考数据:
,试通过计算,判决该汽车在这段限速路上是否超速.(参考数据: 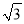 ≈1.7)
≈1.7)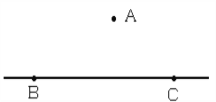
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABC的三个顶点的坐标分别为A(﹣5,3)、B(﹣2,﹣2)、C(﹣3,4).
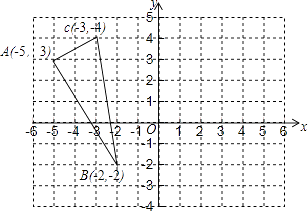
(1)作出△ABC关于y轴对称的△A1B1C1;
(2)写出点A关于x轴对称的点A2的坐标;
(3)△ABC的面积为 .
相关试题

