【题目】如图1,矩形的一条边长为x,周长的一半为y,定义(x,y)为这个矩形的坐标。如图2,在平面直角坐标系中,直线x=1,y=3将第一象限划分成4个区域,已知矩形1的坐标的对应点A落在如图所示的双曲线上,矩形2的坐标的对应点落在区域④中,则下面叙述中正确的是( )

A. 点A的横坐标有可能大于3
B. 矩形1是正方形时,点A位于区域②
C. 当点A沿双曲线向上移动时,矩形1的面积减小
D. 当点A位于区域①时,矩形1可能和矩形2全等
参考答案:
【答案】D
【解析】
A、根据反比例函数k一定,并根据图形得:当x=1时,y<3,得k=xy<3,因为y是矩形周长的一半,即y>x,可判断点A的横坐标不可能大于3;
B、根据正方形边长相等得:y=2x,得点A是直线y=2x与双曲线的交点,画图,如图2,交点A在区域③,可作判断;
C、先表示矩形面积S=x(y-x)=xy-x2=k-x2,当点A沿双曲线向上移动时,x的值会越来越小,矩形1的面积会越来越大,可作判断;
D、当点A位于区域①,得x<1,另一边为:y-x>2,矩形2的坐标的对应点落在区域④中得:x>1,y>3,即另一边y-x>0,可作判断.
如图,设点A(x,y),

A、设反比例函数解析式为:y=![]() (k≠0),
(k≠0),
由图形可知:当x=1时,y<3,
∴k=xy<3,
∵y>x,
∴x<3,即点A的横坐标不可能大于3,
故选项A不正确;
B、当矩形1为正方形时,边长为x,y=2x,
则点A是直线y=2x与双曲线的交点,如图2,交点A在区域③,
故选项B不正确;
C、当一边为x,则另一边为y-x,S=x(y-x)=xy-x2=k-x2,
∵当点A沿双曲线向上移动时,x的值会越来越小,
∴矩形1的面积会越来越大,
故选项C不正确;
D、当点A位于区域①时,
∵点A(x,y),
∴x<1,y>3,即另一边为:y-x>2,
矩形2落在区域④中,x>1,y>3,即另一边y-x>0,
∴当点A位于区域①时,矩形1可能和矩形2全等;
故选项④正确;
故选D.
-
科目: 来源: 题型:
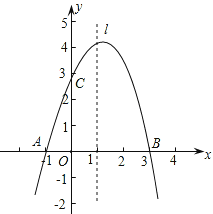
查看答案和解析>>【题目】已知抛物线y=ax2+bx+c经过A(-1,0)、B(3,0)、C(0,3)三点,直线l是抛物线的对称轴.
(1)求抛物线的函数关系式;
(2)设点P是直线l上的一个动点,当△PAC的周长最小时,求点P的坐标;
(3)在直线l上是否存在点M,使△MAC为等腰三角形?若存在,直接写出所有符合条件的点M的坐标;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知⊙O的直径AE=10cm,∠B=∠EAC,则AC的长为( )
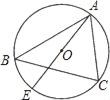
A. 5cm B. 5
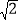 cm C. 5
cm C. 5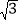 cm D. 6cm
cm D. 6cm -
科目: 来源: 题型:
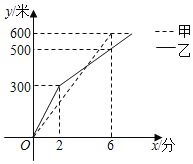
查看答案和解析>>【题目】已知A、B两地相距600米,甲、乙两人同时从A地出发前往B地,所走路程y(米)与行驶时间x(分)之间的函数关系如图所示,则下列说法中:①甲每分钟走100米;②两分钟后乙每分钟走50米;③甲比乙提前3分钟到达B地;④当x=2或6时,甲乙两人相距100米.正确的有_____(在横线上填写正确的序号).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正方形网格中,每个小正方形的边长都为1,点A,点B在网格中的位置如图所示.
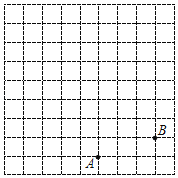
(1)建立适当的直角坐标系,使点A,点B的坐标分别为(1,﹣3),(4,﹣2);
(2)若点C的坐标为(﹣1,﹣1),在平面直角坐标系中画出△ABC;
(3)在图中作出△ABC关于x轴对称的图形△A1B1C1.
-
科目: 来源: 题型:
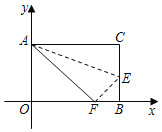
查看答案和解析>>【题目】如图,长方形AOBC,以O为坐标原点,OB、OA分别在x轴、y轴上,点A的坐标为(0,8),点B的坐标为(10,0),点E是BC边上一点,把长方形AOBC沿AE翻折后,C点恰好落在x轴上点F处.
(1)求点E、F的坐标;
(2)求AF所在直线的函数关系式;
(3)在x轴上求一点P,使△PAF成为以AF为腰的等腰三角形,请直接写出所有符合条件的点P的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】曹州牡丹园售票处规定:入园门票每张80元.非节假日的票价打6折售票;节假日根据团队人数实行分段售票:不超过10人,则按原票价购买;超过10人,则其中10人按原票价购买,超过部分的按原票价打8折购买.某旅行社带团x人到牡丹园游览,设非节假日的购票款为y1元,在节假日的购票款为y2元.求:
(1)当x>10时,y1、y2与x的函数关系式;
(2)该旅行社在今年5月1日带甲团与5月10日(非节假日)带乙团到牡丹园游览,甲、乙两个团各25人,请问乙团比甲团便宜多少元?
相关试题

