【题目】如图,将等边![]() 沿
沿![]() 翻折得
翻折得![]() ,
,![]() ,点
,点![]() 为直线
为直线![]() 上的一个动点,连接
上的一个动点,连接![]() ,将线段
,将线段![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() 的角度后得到对应的线段
的角度后得到对应的线段![]() (即
(即![]() ),
),![]() 交
交![]() 于点
于点![]() ,则下列结论:①
,则下列结论:①![]() ;②
;②![]() ;③当
;③当![]() 为线段
为线段![]() 的中点时,则
的中点时,则![]() ;④四边形
;④四边形![]() 的面积为
的面积为![]() ;⑤连接
;⑤连接![]() 、
、![]() ,当
,当![]() 的长度最小时,则
的长度最小时,则![]() 的面积为
的面积为![]() .则说法正确的有________(只填写序号)
.则说法正确的有________(只填写序号)

参考答案:
【答案】①②
【解析】
由等边三角形的性质和折叠的性质,得到四边形ABCD是菱形,则可以判断①、②;当点E时AD中点时,可得△CPF是直角三角形,CE=CF=3,得到![]() ,可以判断③;求出对角线的长度,然后求出菱形的面积,可以判断④;当点E与点A重合时,DF的长度最小,此时四边形ACFD是菱形,求出对角线EF和CD的长度,求出面积,可以判断⑤;即可得到答案.
,可以判断③;求出对角线的长度,然后求出菱形的面积,可以判断④;当点E与点A重合时,DF的长度最小,此时四边形ACFD是菱形,求出对角线EF和CD的长度,求出面积,可以判断⑤;即可得到答案.
解:根据题意,将等边![]() 沿
沿![]() 翻折得
翻折得![]() ,如图:
,如图:
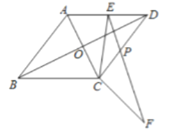
∴![]() ,∠BCD=120°,
,∠BCD=120°,
∴四边形ABCD是菱形,
∴AC⊥BD,AO=CO,BO=DO;故①、②正确;
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴菱形ABCD的面积=![]() ,故④错误;
,故④错误;
当点E时AD中点时,CE⊥AD,
∴DE=![]() ,∠DCE=30°,
,∠DCE=30°,
∴![]() ,
,
∵![]() ,
,
∠PCF=120°![]() ,∠F=30°,
,∠F=30°,
∴![]() ,故③错误;
,故③错误;
当点E与点A重合时,DF的长度最小,如图:
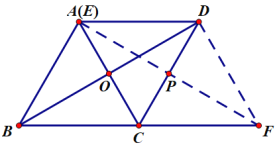
∵AD∥CF,AD=AC=CF,
∴四边形ACFD是菱形,
∴CD⊥EF,CD=![]() ,
,![]() ,
,
∴![]() ;故⑤错误;
;故⑤错误;
∴说法正确的有:①②;
故答案为:①②.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某地农民一直保持着冬种油菜的习惯,利用农闲冬种一季油菜该地农业部门对2017年的油菜籽的生产成本、市场价格、种植面积和产量等进行了统计,并绘制了如下的统计表与统计图(如图):

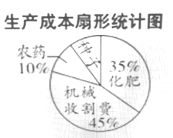
请根据以上信息解答下列问题:
(1)种植每亩油菜所需种子的成本是多少元?
(2)农民冬种油菜每亩获利多少元?
(3)2017年该地全县农民冬种油菜的总获利是多少元?(结果用科学记数法表示).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
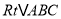 中,
中,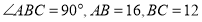 ,点
,点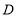 为
为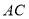 边上的动点,点
边上的动点,点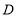 从点
从点 出发,沿边
出发,沿边 向点
向点 运动,当运动到点
运动,当运动到点 时停止,若设点
时停止,若设点 运动的时间为
运动的时间为 秒,点
秒,点 运动的速度为每秒2个单位长度.
运动的速度为每秒2个单位长度.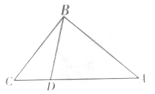

(1)当
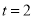 时,
时,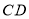 = ,
= ,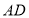 = ;
= ;(2)求当
 为何值时,
为何值时, 是直角三角形,说明理由;
是直角三角形,说明理由;(3)求当
 为何值时,
为何值时,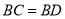 ,并说明理由.
,并说明理由. -
科目: 来源: 题型:
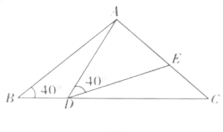
查看答案和解析>>【题目】如图,在等腰
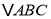 中,
中,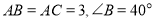 ,点
,点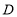 在线段
在线段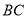 上运动(
上运动(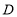 不与
不与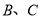 重合),连结
重合),连结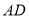 ,作
,作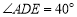 ,
,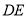 交线段
交线段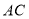 于点
于点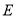 .
.
(1)当
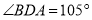 时,
时,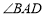 = °;点
= °;点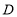 从点
从点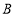 向点
向点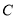 运动时,
运动时,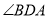 逐渐变 (填“大”或“小”);
逐渐变 (填“大”或“小”);(2)当
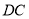 等于多少时,
等于多少时,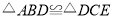 ,请说明理由;
,请说明理由;(3)在点
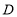 的运动过程中,
的运动过程中,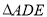 的形状也在改变,判断当
的形状也在改变,判断当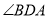 等于多少度时,
等于多少度时,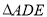 是等腰三角形.
是等腰三角形. -
科目: 来源: 题型:
查看答案和解析>>【题目】2019年是中国建国70周年,作为新时期的青少年,我们应该肩负起实现祖国伟大复兴的责任,为了培养学生的爱国主义情怀,我校学生和老师在5月下旬集体乘车去抗日战争纪念馆研学,已知学生的人数是老师人数的12倍多20人,学生和老师总人数有540人.
(1)请求出去抗日战争纪念馆研学的学生和老师的人数各是多少?
(2)如果学校准备租赁
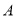 型车和
型车和 型车共14辆(其中
型车共14辆(其中 型车最多7辆),已知
型车最多7辆),已知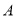 型车每年最车可以载35人,
型车每年最车可以载35人, 型车每车最多可以载45人,共有几种租车方案?
型车每车最多可以载45人,共有几种租车方案?(3)已知
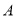 型车日租金为2000元,
型车日租金为2000元, 型车日租金为3000元,设租赁
型车日租金为3000元,设租赁 型大巴车
型大巴车 辆,求出租赁总租金为
辆,求出租赁总租金为 元与
元与 的函数解析式,并求出最经济的租车方案.
的函数解析式,并求出最经济的租车方案. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,已知
 ,
, ,且
,且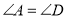 ,
,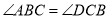 .
.
(1)求证:
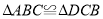 ;
;(2)如图2,若
 ,
, ,折叠纸片,使点
,折叠纸片,使点 与点
与点 重合,折痕为
重合,折痕为 ,且
,且 .
.①求证:
 ;
;②点
 是线段
是线段 上一点,连接
上一点,连接 ,一动点
,一动点 从点
从点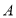 出发,沿线段
出发,沿线段 以每秒1个单位的速度运动到点
以每秒1个单位的速度运动到点 ,再沿线段
,再沿线段 以每秒
以每秒 个单位的速度运动到
个单位的速度运动到 后停止,点
后停止,点 在整个运动过程中用时最少多少秒?
在整个运动过程中用时最少多少秒? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点
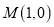 ,过点
,过点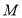 做直线
做直线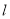 平行于
平行于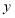 轴,点
轴,点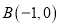 关于直线
关于直线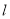 对称点为
对称点为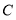 .
.
(1)求点
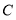 的坐标;
的坐标;(2)点
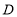 在直线
在直线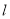 上,且位于
上,且位于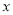 轴的上方,将
轴的上方,将 沿直线
沿直线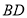 翻折得到
翻折得到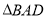 ,若点
,若点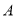 恰好落在直线
恰好落在直线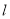 上,求点
上,求点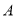 的坐标和直线
的坐标和直线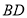 的解析式;
的解析式;(3)设点
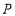 在直线
在直线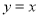 上,点
上,点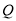 在直线
在直线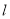 上,当
上,当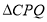 为等边三角形时,求点
为等边三角形时,求点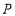 的坐标.
的坐标.
相关试题

