【题目】如图①，已知二次函数的解析式是y＝ax2＋bx(a>0)，顶点为A(1，－1)．

(1)a＝ ；

(2)若点P在对称轴右侧的二次函数图像上运动，连结OP，交对称轴于点B，点B关于顶点A的对称点为C，连接PC、OC，求证：∠PCB＝∠OCB；

(3)如图②，将抛物线沿直线y＝－x作n次平移(n为正整数，n≤12)，顶点分别为A1，A2，…，An，横坐标依次为1，2，…，n，各抛物线的对称轴与x轴的交点分别为D1，D2，…，Dn，以线段AnDn为边向右作正方形AnDnEnFn，是否存在点Fn恰好落在其中的一个抛物线上，若存在，求出所有满足条件的正方形边长；若不存在，请说明理由．

参考答案：

【答案】（1）1；（2）证明见解析；（3）2，6．

【解析】

试题分析：（1）直接利用顶点坐标，进而代入求出即可；

（2）根据题意得出，，进而得出△ODC∽△PHC，求出即可；

（3）由题意得出：A1（1，-1），A2（2，-2），A3（3，-3），…An（n，-n），进而得出F1（2，-1），F2（4，-2），F3（6，-3），…Fn（2n，-n）..，即可分类讨论得出n的值．

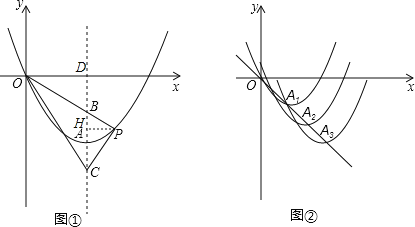
试题解析：（1）解：∵二次函数的解析式是y=ax2+bx（a＞0），顶点为A（1，-1），

∴，

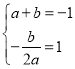解得：．

（2）证明：由（1）得，抛物线的解析式为：y=x2-2x，

设P（m，m2-2m），则直线OP的解析式为：y=（m-2）x，

∴B（1，m-2），∴C（1，-m），

过点P作PH⊥CD于点H，则PH=m-1，CH=m2-m，

∴，，

∵∠ODC=∠PHC，

∴△ODC∽△PHC，

∴∠PCB=∠OCB；

（3）解：由题意得出：A1（1，-1），A2（2，-2），A3（3，-3），…An（n，-n），

∴F1（2，-1），F2（4，-2），F3（6，-3），…Fn（2n，-n）…

若Fn恰好落在其中的第m个抛物线上（m为正整数，m≤12），

则该抛物线解析式为：y=（x-m）2-m，

将Fn代入得：-n=（2n-m）2-m，

即（2n-m）2=m-n，

∴m-n是一个平方数，只能是0，1，4，9，

当m-n=0时，2n-m=0，∴m=n=0（舍去）；

当m-n=1时，2n-m=1或-1，∴n=2或0（舍去）；

当m-n=4时，2n-m=2或-2，∴n=2或6；

当m-n=9时，2n-m=3或-3，∴n=6（舍去）或12（舍去）．

综上所述，正方形边长n的值可以是2，6．

关闭