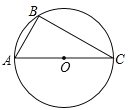
【题目】如图,AC是⊙O的直径,点B在⊙O上,∠ACB=30°.
(1)利用尺规作∠ABC的平分线BD,交AC于点E,交⊙O于点D,连接CD(保留作图痕迹,不写作法);
(2)在(1)所作的图形中,求△ABE与△CDE的面积之比.
参考答案:
【答案】(1)作图见试题解析;(2)![]() .
.
【解析】
试题分析:(1)①以点B为圆心,以任意长为半径画弧,两弧交角ABC两边于点M,N;②分别以点M,N为圆心,以大于![]() MN的长度为半径画弧,两弧交于一点;③作射线BE交AC与E,交⊙O于点D,则线段BD为△ABC的角平分线;
MN的长度为半径画弧,两弧交于一点;③作射线BE交AC与E,交⊙O于点D,则线段BD为△ABC的角平分线;
(2)连接OD,设⊙O的半径为r,可证△ABE∽△DCE,在Rt△ACB中,∠ABC=90°,∠ACB=30°,得到AB=![]() AC=r,得出△ADC是等腰直角三角形,在Rt△ODC中,得出DC=
AC=r,得出△ADC是等腰直角三角形,在Rt△ODC中,得出DC=![]() =
=![]() ,由相似三角形面积比等于相似比的平方即可得到结论.
,由相似三角形面积比等于相似比的平方即可得到结论.
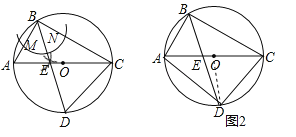
试题解析:(1)如图所示;
(2)如图2,连接OD,设⊙O的半径为r,∵∠BAE=∠CDE,∠AEB=∠DEC,∴△ABE∽△DCE,在Rt△ACB中,∠ABC=90°,∠ACB=30°,∴AB=![]() AC=r,∵∠ABD=∠ACD=45°,∵OD=OC,∴∠ABD=∠ACD=45°,∴∠DOC=90°,在Rt△ODC中,DC=
AC=r,∵∠ABD=∠ACD=45°,∵OD=OC,∴∠ABD=∠ACD=45°,∴∠DOC=90°,在Rt△ODC中,DC=![]() =
=![]() ,∴
,∴![]() =
=![]() =
=![]() =
=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1)(-28 )-(-22)-(-17
)-(-22)-(-17  )+(-22);
)+(-22);
(2)(-100)÷(-5)2-(-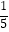 )×[34+(-32)].
)×[34+(-32)]. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知,直线AB∥DC,点P为平面上一点,连接AP与CP.
(1)如图1,点P在直线AB、CD之间,当∠BAP=60°,∠DCP=20°时,求∠APC.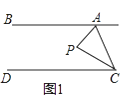
(2)如图2,点P在直线AB、CD之间,∠BAP与∠DCP的角平分线相交于点K,写出∠AKC与∠APC之间的数量关系,并说明理由.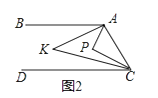
(3)如图3,点P落在CD外,∠BAP与∠DCP的角平分线相交于点K,∠AKC与∠APC有何数量关系?并说明理由.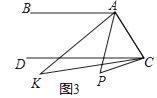
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列二元一次方程组的解为
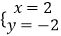 的是( )
的是( )
A.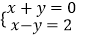
B.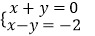
C.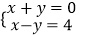
D.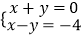
-
科目: 来源: 题型:
查看答案和解析>>【题目】解不等式组
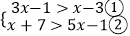 ,并把解集表示在数轴上.[注意有①②]
,并把解集表示在数轴上.[注意有①②] 
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点E、F分别为正方形ABCD中AB、BC边的中点,连接AF、DE相交于点G,连接CG,则tan∠CGD=
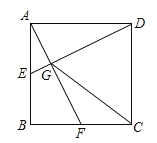
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,小方格边长为1个单位,
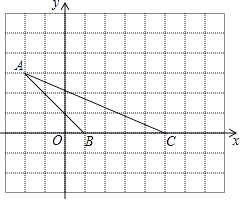
(1)请写出△ABC各点的坐标.
(2)求出S△ABC .
(3)若把△ABC向上平移2个单位,再向右平移2个单位△A′B′C′,在图中画出△A′B′C′.
相关试题

