【题目】已知,直线AB∥DC,点P为平面上一点,连接AP与CP.
(1)如图1,点P在直线AB、CD之间,当∠BAP=60°,∠DCP=20°时,求∠APC.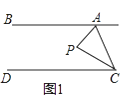
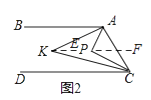
(2)如图2,点P在直线AB、CD之间,∠BAP与∠DCP的角平分线相交于点K,写出∠AKC与∠APC之间的数量关系,并说明理由.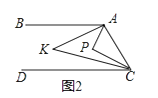
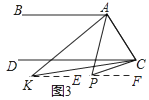
(3)如图3,点P落在CD外,∠BAP与∠DCP的角平分线相交于点K,∠AKC与∠APC有何数量关系?并说明理由.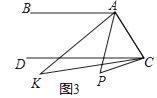
参考答案:
【答案】
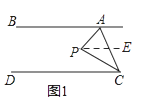
(1)解:如图1,过P作PE∥AB,
∵AB∥CD,
∴PE∥AB∥CD,
∴∠APE=∠BAP,∠CPE=∠DCP,
∴∠APC=∠APE+∠CPE=∠BAP+∠DCP=60°+20°=80°;
(2)解:∠AKC= ![]() ∠APC.
∠APC.
理由:如图2,过K作KE∥AB,
∵AB∥CD,
∴KE∥AB∥CD,
∴∠AKE=∠BAK,∠CKE=∠DCK,
∴∠AKC=∠AKE+∠CKE=∠BAK+∠DCK,
过P作PF∥AB,
同理可得,∠APC=∠BAP+∠DCP,
∵∠BAP与∠DCP的角平分线相交于点K,
∴∠BAK+∠DCK= ![]() ∠BAP+
∠BAP+ ![]() ∠DCP=
∠DCP= ![]() (∠BAP+∠DCP)=
(∠BAP+∠DCP)= ![]() ∠APC,
∠APC,
∴∠AKC= ![]() ∠APC;
∠APC;
(3)解:∠AKC= ![]() ∠APC.
∠APC.
理由:如图3,过K作KE∥AB,
∵AB∥CD,
∴KE∥AB∥CD,
∴∠BAK=∠AKE,∠DCK=∠CKE,
∴∠AKC=∠AKE﹣∠CKE=∠BAK﹣∠DCK,
过P作PF∥AB,
同理可得,∠APC=∠BAP﹣∠DCP,
∵∠BAP与∠DCP的角平分线相交于点K,
∴∠BAK﹣∠DCK= ![]() ∠BAP﹣
∠BAP﹣ ![]() ∠DCP=
∠DCP= ![]() (∠BAP﹣∠DCP)=
(∠BAP﹣∠DCP)= ![]() ∠APC,
∠APC,
∴∠AKC= ![]() ∠APC.
∠APC.
【解析】(1)先过P作PE∥AB,根据平行线的性质即可得到∠APE=∠BAP,∠CPE=∠DCP,再根据∠APC=∠APE+∠CPE=∠BAP+∠DCP进行计算即可;(2)过K作KE∥AB,平行公理的推理可得到KE∥AB∥CD,可得∠AKE=∠BAK,∠CKE=∠DCK,进而得到∠AKC=∠AKE+∠CKE=∠BAK+∠DCK,同理可得,∠APC=∠BAP+∠DCP,再根据角平分线的定义得出∠BAK+∠DCK=![]() ∠BAP+
∠BAP+![]() ∠DCP,进而可得到问题的答案;
∠DCP,进而可得到问题的答案;
(3)过K作KE∥AB,依据平行公理的推理可得到KE∥AB∥CD,可得∠BAK=∠AKE,∠DCK=∠CKE,进而得到∠AKC=∠AKE-∠CKE=∠BAK-∠DCK,同理可得,∠APC=∠BAP-∠DCP,再根据角平分线的定义,得出∠BAK-∠DCK=![]() ∠BAP-
∠BAP-![]() ∠DCP=
∠DCP=![]() (∠BAP-∠DCP)=
(∠BAP-∠DCP)=![]() ∠APC,进而得到∠AKC=
∠APC,进而得到∠AKC=![]() ∠APC.
∠APC.
【考点精析】认真审题,首先需要了解平行线的性质(两直线平行,同位角相等;两直线平行,内错角相等;两直线平行,同旁内角互补).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,OA=2,以点A为圆心,1为半径画⊙A与OA的延长线交于点C,过点A画OA的垂线,垂线与⊙A的一个交点为B,连接BC
(1)线段BC的长等于 ;
(2)请在图中按下列要求逐一操作,并回答问题:
①以点 为圆心,以线段 的长为半径画弧,与射线BA交于点D,使线段OD的长等于
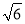 ;
;②连OD,在OD上画出点P,使OP得长等于
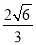 ,请写出画法,并说明理由.
,请写出画法,并说明理由.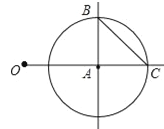
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一个等腰三角形两边长分别为3,7,那么它的周长是( )
A. 17 B. 13 C. 13或17 D. 10或13
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1)(-28 )-(-22)-(-17
)-(-22)-(-17  )+(-22);
)+(-22);
(2)(-100)÷(-5)2-(-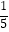 )×[34+(-32)].
)×[34+(-32)]. -
科目: 来源: 题型:
查看答案和解析>>【题目】下列二元一次方程组的解为
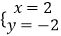 的是( )
的是( )
A.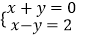
B.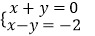
C.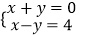
D.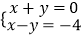
-
科目: 来源: 题型:
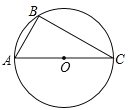
查看答案和解析>>【题目】如图,AC是⊙O的直径,点B在⊙O上,∠ACB=30°.
(1)利用尺规作∠ABC的平分线BD,交AC于点E,交⊙O于点D,连接CD(保留作图痕迹,不写作法);
(2)在(1)所作的图形中,求△ABE与△CDE的面积之比.
-
科目: 来源: 题型:
查看答案和解析>>【题目】解不等式组
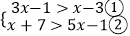 ,并把解集表示在数轴上.[注意有①②]
,并把解集表示在数轴上.[注意有①②] 
相关试题

