【题目】如图,A(1,0)、B(7,0),⊙A、⊙B的半径分别为1和2,将⊙A沿x轴向右平移3个单位,则此时该圆与⊙B的位置关系是( ) 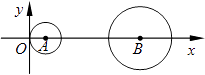
A.外切
B.相交
C.内含
D.外离
参考答案:
【答案】A
【解析】解:∵A(1,0)、B(7,0),⊙A、⊙B的半径分别为1和2, ∴⊙A、⊙B的圆心距为6,
∴⊙A沿x轴向右平移3个单位后,⊙A、⊙B的圆心距为3,
∴根据圆心距与半径之间的数量关系可知两圆的位置关系是外切.
故选A.
【考点精析】根据题目的已知条件,利用圆与圆的位置关系的相关知识可以得到问题的答案,需要掌握两圆之间有五种位置关系:无公共点的,一圆在另一圆之外叫外离,在之内叫内含;有唯一公共点的,一圆在另一圆之外叫外切,在之内叫内切;有两个公共点的叫相交.两圆圆心之间的距离叫做圆心距.两圆的半径分别为R和r,且R≥r,圆心距为P:外离P>R+r;外切P=R+r;相交R-r<P<R+r;内切P=R-r;内含P<R-r.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD的对角线AC,BD相交于点O,延长CB至点F,使CF=CA,连接AF,∠ACF的平分线分别交AF,AB,BD于点E,N,M,连接EO.

(1)已知BD= ,求正方形ABCD的边长;
,求正方形ABCD的边长;
(2)猜想线段CM与CN的数量关系并加以证明. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知抛物线y=ax2+bx+1经过点(2,6),且与直线
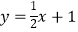 相交于A,B两点,点A在y轴上,过点B作BC⊥x轴,垂足为点C(4,0).
相交于A,B两点,点A在y轴上,过点B作BC⊥x轴,垂足为点C(4,0).
(1)求抛物线的解析式;
(2)若P是直线AB上方该抛物线上的一个动点,过点P作PD⊥x轴于点D,交AB于点E,求线段PE的最大值;
(3)在(2)的条件,设PC与AB相交于点Q,当线段PC与BE相互平分时,请求出点Q的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB∥CD,AC与BD相交于点O,∠A=30°,∠COD=105°.则∠D的大小是( )

A.30°
B.45°
C.65°
D.75° -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,∠A=36°,AB的垂直平分线DE交AC于D,交AB于E,下述结论错误的是( )

A.BD平分∠ABC
B.△BCD的周长等于AB+BC
C.AD=BD=BC
D.点D是线段AC的中点 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平行四边形ABCD中,E为AB的中点,F为AD上一点,EF交AC于G,AF=2cm,DF=4cm,AG=3cm,则AC的长为( )

A.9cm
B.14cm
C.15cm
D.18cm -
科目: 来源: 题型:
查看答案和解析>>【题目】如图是二次函数y1=ax2+bx+c(a≠0)和一次函数y2=mx+n(m≠0)的图象,当y2>y1 , x的取值范围是 .

相关试题

