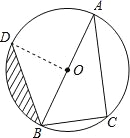
【题目】已知:如图,AB为⊙O的直径,点C、D在⊙O上,且BC=6cm,AC=8cm,∠ABD=45°.(1)求BD的长;
(2)求图中阴影部分的面积.

参考答案:
【答案】(1)BD=![]() =
=![]() cm.
cm.
(2)S阴影=![]() cm2.
cm2.
【解析】
试题分析:(1)由AB为⊙O的直径,得到∠ACB=90°,由勾股定理求得AB,OB=5cm.连OD,得到等腰直角三角形,根据勾股定理即可得到结论;
(2)根据S阴影=S扇形﹣S△OBD即可得到结论.
试题解析:(1)∵AB为⊙O的直径,
∴∠ACB=90°,
∵BC=6cm,AC=8cm,
∴AB=10cm.
∴OB=5cm.
连OD,
∵OD=OB,
∴∠ODB=∠ABD=45°.
∴∠BOD=90°.
∴BD=![]() =
=![]() cm.
cm.
(2)S阴影=S扇形﹣S△OBD=![]() π52﹣
π52﹣![]() ×5×5=
×5×5=![]() cm2.
cm2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(本小题满分11分)学之道在于悟.希望同学们在问题(1)解决过程中有所悟,再继续探索研究问题(2).
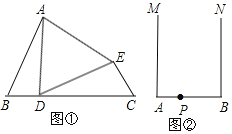
(1)如图①,∠B=∠C,BD=CE,AB=DC.
①求证:△ADE为等腰三角形.
②若∠B=60°,求证:△ADE为等边三角形.
(2)如图②,射线AM与BN,AM⊥AB,BN⊥AB,点P是AB上一点,在射线AM与BN上分别作点C、点D满足:△CPD为等腰直角三角形.(要求:利用直尺与圆规,不写作法,保留作图痕迹)
-
科目: 来源: 题型:
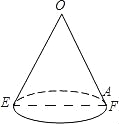
查看答案和解析>>【题目】如图是一个用来盛爆米花的圆锥形纸杯,纸杯开口圆的直径EF长为10cm,母线OE(OF)长为10cm.在母线OF上的点A处有一块爆米花残渣,且FA=2cm,一只蚂蚁从杯口的点E处沿圆锥表面爬行到A点,则此蚂蚁爬行的最短距离 cm.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知ab<0,且|a|<|b|,化简|a+b|+|a﹣b|+|b﹣a|=_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若a是有理数,则计算正确的是( )
A. (﹣a)+(﹣a)=2a B. ﹣a+(﹣a)=0
C. (﹣a)﹣(﹣a)=2a D. ﹣a﹣(+a)=﹣2a
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列计算正确的是( )
A.2x+x=2x2
B.2x2﹣x2=2
C.2x23x2=6x4
D.2x6÷x2=2x3 -
科目: 来源: 题型:
查看答案和解析>>【题目】(本小题满分9分)课本的作业题中有这样一道题:把一张顶角为36°的等腰三角形纸片剪两刀,分成3张小纸片,使每张小纸片都是等腰三角形,你能办到吗?请画示意图说明剪法.
我们有多少种剪法,图1是其中的一种方法:
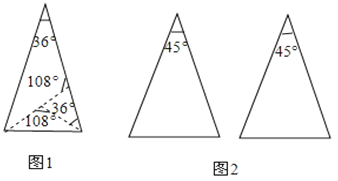
定义:如果两条线段将一个三角形分成3个等腰三角形,我们把这两条线段叫做这个三角形的三分线.
(1)请你在图2中用两种不同的方法画出顶角为45°的等腰三角形的三分线,并标注每个等腰三角形顶角的度数;(若两种方法分得的三角形成3对全等三角形,则视为同一种)
(2)
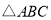 中,∠B=30°,AD和DE是
中,∠B=30°,AD和DE是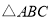 的三分线,点D在BC边上,点E在AC边上,且AD=BD,DE=CE,设∠C=x°,试画出示意图,并求出x所有可能的值.
的三分线,点D在BC边上,点E在AC边上,且AD=BD,DE=CE,设∠C=x°,试画出示意图,并求出x所有可能的值.
相关试题

