【题目】(本小题满分11分)学之道在于悟.希望同学们在问题(1)解决过程中有所悟,再继续探索研究问题(2).
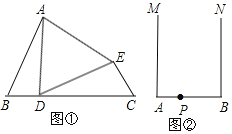
(1)如图①,∠B=∠C,BD=CE,AB=DC.
①求证:△ADE为等腰三角形.
②若∠B=60°,求证:△ADE为等边三角形.
(2)如图②,射线AM与BN,AM⊥AB,BN⊥AB,点P是AB上一点,在射线AM与BN上分别作点C、点D满足:△CPD为等腰直角三角形.(要求:利用直尺与圆规,不写作法,保留作图痕迹)
参考答案:
【答案】见解析
【解析】(1)①在△ABD和△DCE中,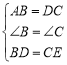 ,
,
∴△ABD≌△DCE(SAS),∴AD=DE,即△ADE为等腰三角形;(2分)
②∵△ABD≌△DCE,∴∠BAD=∠CDE,
∵∠B=60°,∴∠BAD+∠ADB=120°,∴∠CDE+∠ADB=120°,
∴∠ADE=60°,又∵△ADE为等腰三角形,∴△ADE为等边三角形;(5分)
(2)有三种情况,PC=PD、CP=CD、DC=DP,如图所示:
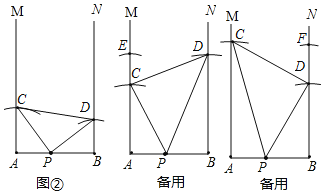 (11分)
(11分)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,D、E分别为AB、AC上两点,将△ABC沿直线DE折叠,使得点A落在△ABC右侧的A1处,则∠A、∠1、∠2之间满足的关系式是( )
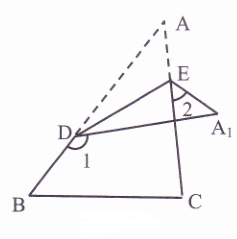
A.∠A=∠1-∠2
B.∠A= ∠1-∠2
∠1-∠2
C.∠A=∠1-2∠2
D.2∠A=∠1-∠2 -
科目: 来源: 题型:
查看答案和解析>>【题目】一元二次方程x2=3x的解是: .
-
科目: 来源: 题型:
查看答案和解析>>【题目】3,5,8,9,7,6,2的中位数是_____.
-
科目: 来源: 题型:
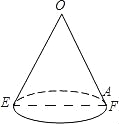
查看答案和解析>>【题目】如图是一个用来盛爆米花的圆锥形纸杯,纸杯开口圆的直径EF长为10cm,母线OE(OF)长为10cm.在母线OF上的点A处有一块爆米花残渣,且FA=2cm,一只蚂蚁从杯口的点E处沿圆锥表面爬行到A点,则此蚂蚁爬行的最短距离 cm.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知ab<0,且|a|<|b|,化简|a+b|+|a﹣b|+|b﹣a|=_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,AB为⊙O的直径,点C、D在⊙O上,且BC=6cm,AC=8cm,∠ABD=45°.(1)求BD的长;
(2)求图中阴影部分的面积.

相关试题

