搜索
【题目】已知线段AB=8cm，点C是直线AB上一点，线段BC=3cm，D、E分别是线段AB与线段CB的中点，求线段DE的长度．
参考答案：
【答案】解：（1）如图1，
，
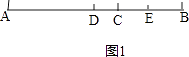8÷2﹣3÷2
=4﹣1.5
=2.5（cm）
所以线段DE的长度是2.5cm．
（ 2 ）如图2，
，
8÷2+3÷2
=4+1.5
=5.5（cm）
所以线段DE的长度是5.5cm．
综上，可得线段DE的长度是2.5cm或5.5cm
【解析】抓住已知点C是直线AB上一点，因此分两种情况：当点C在线段AB上，根据点D是线段AB的中点求出DB的长，再根据E是线段CB的中点求出BE的长，再根据DE=DB-BE即可求得结果；当点C在线段AB的延长线上时，根据点D是线段AB的中点求出DB的长，再根据E是线段CB的中点求出BE的长，再根据DE=DB+BE即可求得结果。
-
科目： 来源： 题型：
查看答案和解析>>【题目】比1小2的数是（ ）
A. -1 B. -2 C. -3 D. 0
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，将等腰△ABC绕顶点B逆时针方向旋转α度到△A1B1C1的位置，AB与A1C1相交于点D，AC与A1C1、BC1分别交于点E、F．
（1）求证：△BCF≌△BA1D；
（2）当∠C=α度时，判定四边形A1BCE的形状，并说明理由．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，O为直线AB上一点，∠AOC=50°，OD平分∠AOC，∠DOE=90度．
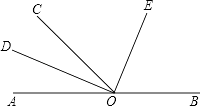
（1）请你数一数，图中有多少个角；
（2）求出∠BOD的度数；
（3）请通过计算说明OE是否平分∠BOC． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，四边形ABCD为平行四边形，∠BAD的角平分线AF交CD于点E，交BC的延长线于点F．
（1）求证：BF=CD；
（2）连接BE，若BE⊥AF，∠BFA=60°，BE=
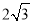，求平行四边形ABCD的周长．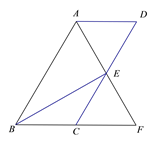
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在△ABC中，AB=AC，△ABC与△DEC关于点C成中心对称，连接AE、BD．
（1）线段AE、BD具有怎样的位置关系和大小关系？说明你的理由．
（2）如果△ABC的面积为5cm2 ， 求四边形ABDE的面积．
（3）当∠ACB为多少度时，四边形ABDE为矩形？说明你的理由．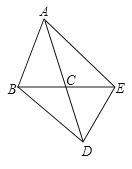
-
科目： 来源： 题型：
查看答案和解析>>【题目】在等腰△ABC中，
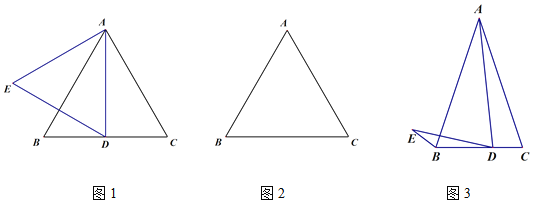
（1）如图1，若△ABC为等边三角形，D为线段BC中点，线段AD关于直线AB的对称线段为线段AE，连接DE，则∠BDE的度数为___________；
（2）若△ABC为等边三角形，点D为线段BC上一动点（不与B，C重合），连接AD并将线段AD绕点D逆时针旋转60°得到线段DE，连接BE.
①根据题意在图2中补全图形；
②小玉通过观察、验证，提出猜测：在点D运动的过程中，恒有CD=BE.经过与同学们的充分讨论，形成了几种证明的思路：
思路1：要证明CD=BE，只需要连接AE，并证明△ADC≌△AEB；
思路2：要证明CD=BE，只需要过点D作DF∥AB，交AC于F，证明△ADF≌△DEB；
思路3：要证明CD=BE，只需要延长CB至点G，使得BG=CD，证明△ADC≌△DEG；
……
请参考以上思路，帮助小玉证明CD=BE.（只需要用一种方法证明即可）
（3）小玉的发现启发了小明：如图3，若AB=AC=kBC，AD=kDE，且∠ADE=∠C，此时小明发现BE，BD，AC三者之间满足一定的的数量关系，这个数量关系是______________________.（直接给出结论无须证明）
相关试题
