【题目】如图,将等腰△ABC绕顶点B逆时针方向旋转α度到△A1B1C1的位置,AB与A1C1相交于点D,AC与A1C1、BC1分别交于点E、F.
(1)求证:△BCF≌△BA1D;
(2)当∠C=α度时,判定四边形A1BCE的形状,并说明理由.

参考答案:
【答案】(1)证明见解析;(2)四边形A1BCE是菱形.
【解析】
试题分析:(1)根据等腰三角形的性质得到AB=BC,∠A=∠C,由旋转的性质得到A1B=AB=BC,∠A=∠A1=∠C,∠A1BD=∠CBC1,根据全等三角形的判定定理得到△BCF≌△BA1D;
(2)由旋转的性质得到∠A1=∠A,根据平角的定义得到∠DEC=180°﹣α,根据四边形的内角和得到∠ABC=360°﹣∠A1﹣∠C﹣∠A1EC=180°﹣α,证得四边形A1BCE是平行四边形,由于A1B=BC,即可得到四边形A1BCE是菱形.
试题解析:(1)证明:∵△ABC是等腰三角形,∴AB=BC,∠A=∠C,∵将等腰△ABC绕顶点B逆时针方向旋转α度到△A1B1C1的位置,∴A1B=AB=BC,∠A=∠A1=∠C,∠A1BD=∠CBC1,在△BCF与△BA1D中,∵∠A1=∠C,A1B=BC,∠A1BD=∠CBF,∴△BCF≌△BA1D;
(2)解:四边形A1BCE是菱形,∵将等腰△ABC绕顶点B逆时针方向旋转α度到△A1B1C1的位置,∴∠A1=∠A,∵∠ADE=∠A1DB,∴∠AED=∠A1BD=α,∴∠DEC=180°﹣α,∵∠C=α,∴∠A1=α,∴∠ABC=360°﹣∠A1﹣∠C﹣∠A1EC=180°﹣α,∴∠A1=∠C,∠A1BC=∠AEC,∴四边形A1BCE是平行四边形,∴A1B=BC,∴四边形A1BCE是菱形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】找出图中的旋转中心,说出旋转多少度能与原图形重合?并说出它是否是中心对称图形.
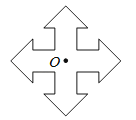
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个菱形的两条对角线的长分别为5和8,那么这个菱形的面积是( )
A. 40 B. 20 C. 10 D. 25
-
科目: 来源: 题型:
查看答案和解析>>【题目】比1小2的数是( )
A. -1 B. -2 C. -3 D. 0
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,O为直线AB上一点,∠AOC=50°,OD平分∠AOC,∠DOE=90度.
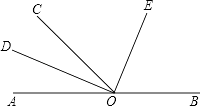
(1)请你数一数,图中有多少个角;
(2)求出∠BOD的度数;
(3)请通过计算说明OE是否平分∠BOC. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知线段AB=8cm,点C是直线AB上一点,线段BC=3cm,D、E分别是线段AB与线段CB的中点,求线段DE的长度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD为平行四边形,∠BAD的角平分线AF交CD于点E,交BC的延长线于点F.
(1)求证:BF=CD;
(2)连接BE,若BE⊥AF,∠BFA=60°,BE=
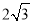 ,求平行四边形ABCD的周长.
,求平行四边形ABCD的周长.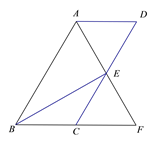
相关试题

