Question

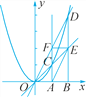
【题目】如图，在x轴上有两点A(m，0)，B(n，0)(n>m>0)，分别过点A，B作x轴的垂

线交抛物线y＝x2于点C，D，直线OC交直线BD于点E，直线OD交直线AC于点F.点E，F的纵坐标分别为yE，yF.

(1)特例探究(填空)：

当m＝1，n＝2时，yE＝____，yF＝____；

当m＝3，n＝5时，yE＝____，yF＝____．

(2)归纳证明：对任意m,n(n>m>0)，猜想yE与yF的大小关系，并证明你的猜想．

(3)拓展应用：连结EF，AE，当S四边形OFEB＝3S△OFE时，直接写出m与n的关系及四边形OFEA的形状．

Answer 1

【答案】(1) 当m＝1，n＝2时，yE＝__2__， ＝__2__；当m＝3，n＝5时， ＝__15__，yF＝__15__．

(2) =.证明见解析．

(3) n＝2m,四边形OFEA为平行四边形.

【解析】分析：（1）已知A、B的坐标，根据抛物线的解析式，能得到C、D的坐标，进而能求出直线OC、OD的解析式，也就能得出E、F两点的坐标，再进行比较即可．（2）已知A、B的坐标，根据抛物线的解析式，能得到C、D的坐标，进而能求出直线OC、OD的解析式，也就能得出E、F两点的坐标，再进行比较即可．（3）四边形OFEA的面积可分作△OEF、△OEA两部分，根据给出的四边形和△OFE的面积比例关系，能判断出EF、OA的比例关系，进而得出m、n的比例关系，再对四边形OFEA的形状进行判定．

本题解析：

(1) 当m＝1，n＝2时，yE＝__2__，yF＝__2__；当m＝3，n＝5时，yE＝__15__，yF＝__15__.

(2)∵点C为抛物线y＝x2上的点，AC⊥x轴，∴xC＝xA＝m，∴点C(m，m2)．

易求得直线yOC＝mx，

又∵xE＝n，∴yE＝mn.

同理，点D(n，n2)，易求得直线yOD＝nx，

∴yF＝nm＝mn.∴yE＝yF.

(3)∵yE＝yF，AF⊥x轴，BE⊥x轴，

∴AF＝BE，AF∥BE，

∴四边形ABEF为平行四边形，

∴EF∥OB，EF＝AB＝n－m.

∴S四边形OFEB＝ (n－m＋n)·yE＝ (2n－m)·yE，S△OFE＝ (n－m)·yE.

∵S四边形OFEB＝3S△OFE，

∴ (2n－m)·yE＝3× (n－m)·yE，

∴2n－m＝3(n－m)，∴n＝2m.

此时EF＝n－m＝2m－m＝m＝OA，

∴EF平行且等于OA，∴四边形OFEA为平行四边形．