【题目】如图,正方形ABCD中,AB=1,以线段BC、CD上两点P、Q和方形的点A为顶点作正方形的内接等边△APQ,求△APQ的边长.
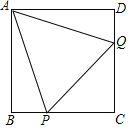
参考答案:
【答案】△APQ的边长为![]() .
.
【解析】
连接AC,交PQ于点H,根据正方形和等边三角形的性质可证Rt△ABP≌Rt△ADQ,可得△CPQ是等腰直角三角形,在直角三角形ABP中,解直角三角形可求得PH,即可求得△APQ的边长.
连接AC,交PQ于点H,
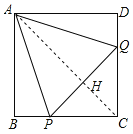
如图所示:则∠BAC=∠DAC=∠BCA=∠DCA=45°,
∵△APQ是等边三角形,
∴AP=AQ=PQ,∠PAQ=60°,
∵四边形ABCD是正方形,
∴AB=AD,∠B=∠D=90°,
在Rt△ABP和Rt△ADQ中,![]() ,
,
∴Rt△ABP≌Rt△ADQ(HL),
∴∠BAP=∠DAQ,BP=DQ,
∴∠PAC=∠QAC,CP=CQ,
∴△CPQ是等腰直角三角形,
∵∠PAQ=60°,
∴∠PAC=∠QAC=30°,
∵∠APQ=60°,
∴∠AHP=90°,
∴PH=QH,
∴CH=PH=QH,AC=![]() AB=
AB=![]() ,
,
PH=tan∠PAHAH=tan30°×(AC﹣CH)=![]() ×(
×(![]() ﹣PH),
﹣PH),
解得:PH=![]() ,
,
∴PQ=2PH=![]() ,
,
∴△APQ的边长为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】书店老板去图书批发市场购买某种图书,第一次用 1200 元购买若干本,按 每本 10 元出售,很快售完.第二次购买时,每本书的进价比第一次提高了 20%,他用1500 元所购买的数量比第一次多 10 本.
(1)求第一次购买的图书,每本进价多少元?
(2)第二次购买的图书,按每本 10 元售出 200 本时,出现滞销,剩下的图书降价后全部 售出,要使这两次销售的总利润不低于 2100 元,每本至多降价多少元?(利润=销售收入一进价)
-
科目: 来源: 题型:
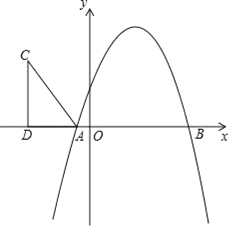
查看答案和解析>>【题目】如图,抛物线y=-x2+bx+c与x轴相交于A(-1,0),B(5,0)两点.
(1)求抛物线的解析式;
(2)在第二象限内取一点C,作CD垂直x轴于点D,链接AC,且AD=5,CD=8,将Rt△ACD沿x轴向右平移m个单位,当点C落在抛物线上时,求m的值;
(3)在(2)的条件下,当点C第一次落在抛物线上记为点E,点P是抛物线对称轴上一点.试探究:在抛物线上是否存在点Q,使以点B、E、P、Q为顶点的四边形是平行四边形?若存在,请出点Q的坐标;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,点 A,B的坐标分别为(0,3),(1,0),△ABC是等腰直角三角形,∠ABC=90°.
(1)图1中,点C的坐标为 ;
(2)如图2,点D的坐标为(0,1),点E在射线CD上,过点B 作BF⊥BE交y轴于点F.
①当点E为线段CD的中点时,求点F的坐标;
②当点E在第二象限时,请直接写出F点纵坐标y的取值范围.

-
科目: 来源: 题型:
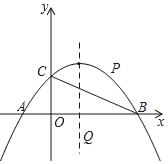
查看答案和解析>>【题目】如图,已知点A(﹣1,0),B(3,0),C(0,1)在抛物线y=ax2+bx+c上.
(1)求抛物线解析式;
(2)在直线BC上方的抛物线上求一点P,使△PBC面积为1;
(3)在x轴下方且在抛物线对称轴上,是否存在一点Q,使∠BQC=∠BAC?若存在,求出Q点坐标;若不存在,说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知一次函数y=kx+k+1的图象与一次函数y=﹣x+4的图象交于点A(1,a).

(1)求a、k的值;
(2)根据图象,写出不等式﹣x+4>kx+k+1的解;
(3)结合图形,当x>2时,求一次函数y=﹣x+4函数值y的取值范围;
-
科目: 来源: 题型:
查看答案和解析>>【题目】某公司的午餐采用自助的形式,并倡导员工“适度取餐,减少浪费”该公司共有10个部门,且各部门的人数相同.为了解午餐的浪费情况,从这10个部门中随机抽取了
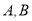 两个部门,进行了连续四周(20个工作日)的调查,得到这两个部门每天午餐浪费饭菜的重量,以下简称“每日餐余重量”(单位:千克),并对这些数据进行了整理、描述和分析.下面给出了部分信息.
两个部门,进行了连续四周(20个工作日)的调查,得到这两个部门每天午餐浪费饭菜的重量,以下简称“每日餐余重量”(单位:千克),并对这些数据进行了整理、描述和分析.下面给出了部分信息. .
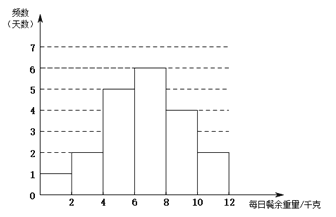
.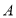 部门每日餐余重量的频数分布直方图如下(数据分成6组:
部门每日餐余重量的频数分布直方图如下(数据分成6组: ,
, ,
,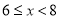 ,
,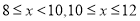 ):
):
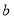 .
.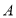 部门每日餐余重量在
部门每日餐余重量在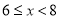 这一组的是:6.1 6.6 7.0 7.0 7.0 7.8
这一组的是:6.1 6.6 7.0 7.0 7.0 7.8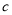 .
.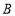 部门每日餐余重量如下:1.4 2.8 6.9 7.8 1.9 9.7 3.1 4.6 6.9 10.8 6.9 2.6 7.5 6.9 9.5 7.8 8.4 8.3 9.4 8.8
部门每日餐余重量如下:1.4 2.8 6.9 7.8 1.9 9.7 3.1 4.6 6.9 10.8 6.9 2.6 7.5 6.9 9.5 7.8 8.4 8.3 9.4 8.8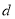 .
. 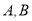 两个部门这20个工作日每日餐余重量的平均数、中位数、众数如下:
两个部门这20个工作日每日餐余重量的平均数、中位数、众数如下:部门
平均数
中位数
众数
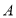
6.4
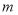
7.0
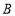 /p>
/p>6.6
7.2

根据以上信息,回答下列问题:
(1)写出表
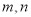 中的值;
中的值;(2)在
 这两个部门中,“适度取餐,减少浪费”做得较好的部门是________(填“
这两个部门中,“适度取餐,减少浪费”做得较好的部门是________(填“ ”或“
”或“ ”),理由是____________;
”),理由是____________;(3)结合
 这两个部门每日餐余重量的数据,估计该公司(10个部门)一年(按240个工作日计算)的餐余总重量.
这两个部门每日餐余重量的数据,估计该公司(10个部门)一年(按240个工作日计算)的餐余总重量.
相关试题

