【题目】完成推理填空:如图在△ABC中,已知∠1+∠2=180°,∠3=∠B,试说明∠AED=∠C.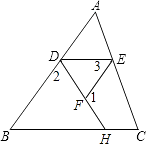
解:∵∠1+∠EFD=180°(邻补角定义),∠1+∠2=180°(已知)
∴(同角的补角相等)①
∴(内错角相等,两直线平行)②
∴∠ADE=∠3()③
∵∠3=∠B()④
∴(等量代换)⑤
∴DE∥BC()⑥
∴∠AED=∠C()⑦
参考答案:
【答案】∠EFD=∠2;AB∥EF;两直线平行,内错角相等;已知;∠ADE=∠B;同位角相等,两直线平行;两直线平行,同位角相等
【解析】∵∠1+∠EFD=180°(邻补角定义),∠1+∠2=180°(已知 )
∴∠EFD=∠2(同角的补角相等)①
∴AB∥EF(内错角相等,两直线平行)②
∴∠ADE=∠3(两直线平行,内错角相等)③
∵∠3=∠B(已知)④
∴∠ADE=∠B(等量代换)⑤
∴DE∥BC(同位角相等,两直线平行)⑥
∴∠AED=∠C(两直线平行,同位角相等)⑦.
答案为:∠EFD=∠2;AB∥EF;两直线平行,内错角相等;
∠ADE=∠B,同位角相等,两直线平;
两直线平行,同位角相等.
【考点精析】关于本题考查的余角和补角的特征和平行线的判定与性质,需要了解互余、互补是指两个角的数量关系,与两个角的位置无关;由角的相等或互补(数量关系)的条件,得到两条直线平行(位置关系)这是平行线的判定;由平行线(位置关系)得到有关角相等或互补(数量关系)的结论是平行线的性质才能得出正确答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠ACB=90°,过点C的直线MN∥AB,D为AB边上一点,过点D作DE⊥BC,交直线MN于E,垂足为F,连接CD、BE.
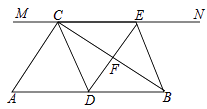
(1)求证:CE=AD;
(2)当D在AB中点时,四边形BECD是什么特殊四边形?说明你的理由;
(3)若D为AB中点,则当∠A的大小满足什么条件时,四边形BECD是正方形?请说明你的理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】用一个平面截去正方体的一个角,则截面不可能是( )
A. 等腰直角三角形 B. 等腰三角形
C. 锐角三角形 D. 等边三角形
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,某高楼顶部有一信号发射塔,小凡在矩形建筑物ABCD的A、C两点处测得塔顶F的仰角分别为α和β,AD=18m,CD=78m.
(1)用α和β的三角函数表示CE;
(2)当α=30°、β=60°时,求EF(结果精确到1m).
(参考数据:
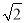 ≈1.414,
≈1.414,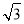 ≈1.732)
≈1.732)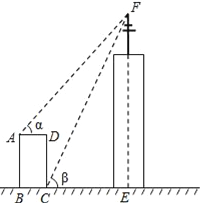
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知矩形OABC中,OA=3,AB=6,以OA,OC所在的直线为坐标轴,建立如图1的平面直角坐标系.将矩形OABC绕点O顺时针方向旋转,得到矩形ODEF,当点B在直线DE上时,设直线DE和x轴交于点P,与y轴交于点Q.
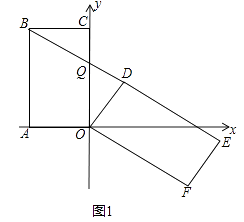
(1)求证:△BCQ≌△ODQ;
(2)求点P的坐标;
(3)若将矩形OABC向右平移(图2),得到矩形ABCG,设矩形ABCG与矩形ODEF重叠部分的面积为S,OG=x,请直接写出x≤3时,S与x之间的函数关系式,并且写出自变量x的取值范围.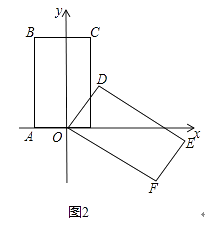
-
科目: 来源: 题型:
查看答案和解析>>【题目】必然事件的概率是( )
A.1B.0C.大于0且小于1D.大于1
-
科目: 来源: 题型:
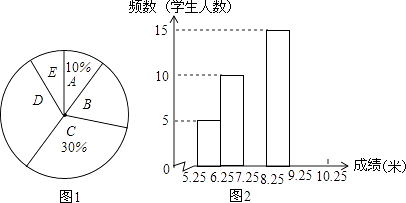
查看答案和解析>>【题目】将七年级两个班男生掷实心球的成绩进行整理,并绘制出频数分布表、扇形统计图和频数分布直方图(不完整).(x表示成绩,且规定x≥6.25为合格,x≥9.25为优秀)
组别
成绩(米)
频数
A
5.25≤x<6.25
5
B
6.25≤x<7.25
10
C
7.25≤x<8.25
a
D
8.25≤x<9.25
15
E
9.25≤x<10.25
b
相关试题

