【题目】如图,在Rt△ABC中,∠ACB=90°,过点C的直线MN∥AB,D为AB边上一点,过点D作DE⊥BC,交直线MN于E,垂足为F,连接CD、BE.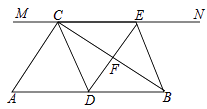
(1)求证:CE=AD;
(2)当D在AB中点时,四边形BECD是什么特殊四边形?说明你的理由;
(3)若D为AB中点,则当∠A的大小满足什么条件时,四边形BECD是正方形?请说明你的理由.
参考答案:
【答案】
(1)
证明:∵DE⊥BC,
∴∠DFB=90°,
∵∠ACB=90°,
∴∠ACB=∠DFB,
∴AC∥DE,
∵MN∥AB,即CE∥AD,
∴四边形ADEC是平行四边形,
∴CE=AD;
(2)
解:四边形BECD是菱形,
理由是:∵D为AB中点,
∴AD=BD,
∵CE=AD,
∴BD=CE,
∵BD∥CE,
∴四边形BECD是平行四边形,
∵∠ACB=90°,D为AB中点,
∴CD=BD,
∴四边形BECD是菱形;
(3)
当∠A=45°时,四边形BECD是正方形,理由是:
解:∵∠ACB=90°,∠A=45°,
∴∠ABC=∠A=45°,
∴AC=BC,
∵D为BA中点,
∴CD⊥AB,
∴∠CDB=90°,
∵四边形BECD是菱形,
∴菱形BECD是正方形,
即当∠A=45°时,四边形BECD是正方形.
【解析】(1)先求出四边形ADEC是平行四边形,根据平行四边形的性质推出即可;(2)求出四边形BECD是平行四边形,求出CD=BD,根据菱形的判定推出即可;(3)求出∠CDB=90°,再根据正方形的判定推出即可.
-
科目: 来源: 题型:
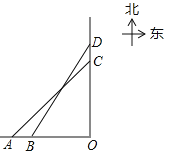
查看答案和解析>>【题目】如图,轮船甲位于码头O的正西方向A处,轮船乙位于码头O的正北方向C处,测得∠CAO=45°,轮船甲自西向东匀速行驶,同时轮船乙沿正北方向匀速行驶,它们的速度分别为45km/h和36km/h,经过0.1h,轮船甲行驶至B处,轮船乙行驶至D处,测得∠DBO=58°,此时B处距离码头O多远?(参考数据:sin58°≈0.85,cos58°≈0.53,tan58°≈1,60)
-
科目: 来源: 题型:
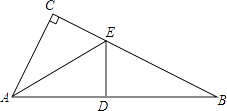
查看答案和解析>>【题目】已知:如图,在△ABC中,∠C=90°,AE是△ABC的角平分线;ED平分∠AEB,交AB于点D;∠CAE=∠B.
(1)求∠B的度数.
(2)如果AC=3cm,求AB的长度.
(3)猜想:ED与AB的位置关系,并证明你的猜想. -
科目: 来源: 题型:
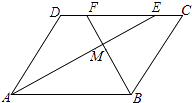
查看答案和解析>>【题目】如图,在ABCD中,AE、BF分别平分∠DAB和∠ABC,交CD于点E、F,AE、BF相交于点M.
(1)试说明:AE⊥BF;
(2)判断线段DF与CE的大小关系,并予以说明. -
科目: 来源: 题型:
查看答案和解析>>【题目】用一个平面截去正方体的一个角,则截面不可能是( )
A. 等腰直角三角形 B. 等腰三角形
C. 锐角三角形 D. 等边三角形
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,某高楼顶部有一信号发射塔,小凡在矩形建筑物ABCD的A、C两点处测得塔顶F的仰角分别为α和β,AD=18m,CD=78m.
(1)用α和β的三角函数表示CE;
(2)当α=30°、β=60°时,求EF(结果精确到1m).
(参考数据:
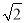 ≈1.414,
≈1.414,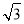 ≈1.732)
≈1.732)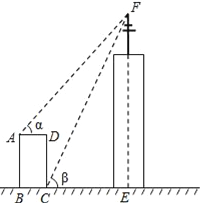
-
科目: 来源: 题型:
查看答案和解析>>【题目】完成推理填空:如图在△ABC中,已知∠1+∠2=180°,∠3=∠B,试说明∠AED=∠C.
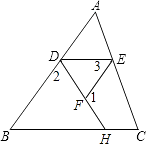
解:∵∠1+∠EFD=180°(邻补角定义),∠1+∠2=180°(已知)
∴(同角的补角相等)①
∴(内错角相等,两直线平行)②
∴∠ADE=∠3()③
∵∠3=∠B()④
∴(等量代换)⑤
∴DE∥BC()⑥
∴∠AED=∠C()⑦
相关试题

