【题目】空地上有一段长为a米的旧墙MN,某人利用旧墙和木栏围成一个矩形菜园ABCD,已知木栏总长为100米.
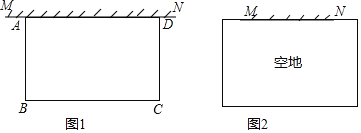
(1)已知a=20,矩形菜园的一边靠墙,另三边一共用了100米木栏,且围成的矩形菜园面积为450平方米.如图1,求所利用旧墙AD的长;
(2)已知0<α<50,且空地足够大,如图2.请你合理利用旧墙及所给木栏设计一个方案,使得所围成的矩形菜园ABCD的面积最大,并求面积的最大值.
参考答案:
【答案】(1)利用旧墙AD的长为10米.(2)见解析.
【解析】
(1)按题意设出AD,表示AB构成方程;
(2)根据旧墙长度a和AD长度表示矩形菜园长和宽,注意分类讨论s与菜园边长之间的数量关系.
(1)设AD=x米,则AB=![]() 米
米
依题意得,![]() =450
=450
解得x1=10,x2=90
∵a=20,且x≤a
∴x=90舍去
∴利用旧墙AD的长为10米.
(2)设AD=x米,矩形ABCD的面积为S平方米
①如果按图一方案围成矩形菜园,依题意
得:
S=![]() ,0<x<a
,0<x<a
∵0<a<50
∴x<a<50时,S随x的增大而增大
当x=a时,S最大=50a-![]() a2
a2
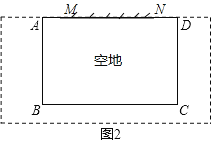
②如按图2方案围成矩形菜园,依题意得
S=![]() ,a≤x<50+
,a≤x<50+![]()
当a<25+![]() <50时,即0<a<
<50时,即0<a<![]() 时,
时,
则x=25+![]() 时,S最大=(25+
时,S最大=(25+![]() )2=
)2=![]() ,
,
当25+![]() ≤a,即
≤a,即![]() ≤a<50时,S随x的增大而减小
≤a<50时,S随x的增大而减小
∴x=a时,S最大=![]() =
=![]() ,
,
综合①②,当0<a<![]() 时,
时,![]() -(
-(![]() )=
)=![]() >0
>0
![]() >
>![]() ,此时,按图2方案围成矩形菜园面积最大,最大面积为
,此时,按图2方案围成矩形菜园面积最大,最大面积为![]() 平方米
平方米
当![]() ≤a<50时,两种方案围成的矩形菜园面积最大值相等.
≤a<50时,两种方案围成的矩形菜园面积最大值相等.
∴当0<a<![]() 时,围成长和宽均为(25+
时,围成长和宽均为(25+![]() )米的矩形菜园面积最大,最大面积为
)米的矩形菜园面积最大,最大面积为![]() 平方米;
平方米;
当![]() ≤a<50时,围成长为a米,宽为(50-
≤a<50时,围成长为a米,宽为(50-![]() )米的矩形菜园面积最大,最大面积为(
)米的矩形菜园面积最大,最大面积为(![]() )平方米.
)平方米.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形
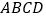 中,
中,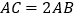 ,将矩形
,将矩形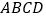 绕点
绕点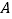 旋转得到矩形
旋转得到矩形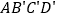 ,使点
,使点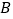 的对应点
的对应点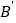 落在
落在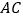 上,
上,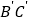 交
交 于点
于点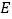 ,在
,在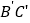 上取点
上取点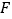 ,使
,使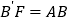 .
.(1)证:
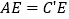 .
.(2)
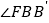 的度数.
的度数.(3)知
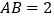 ,求
,求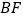 的长.
的长.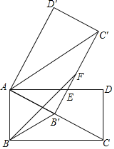
-
科目: 来源: 题型:
查看答案和解析>>【题目】在“全民读书月”活动中,小明调查了班级里40名同学本学期计划购买课外书的花费情况,并将结果绘制成如图所示的统计图,请根据相关信息,解答下列问题:(直接填写结果)

(1)本次调查获取的样本数据的众数是 ;
(2)这次调查获取的样本数据的中位数是 ;
(3)若该校共有学生1000人,根据样本数据,估计本学期计划购买课外书花费50元的学生有 人.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校举办了一次知识竞赛,满分10分,学生得分均为整数,成绩达到6分以上(包括6分)为合格,达到9分以上(包括9分)为优秀.这次竞赛中甲、乙两组学生成绩分布的条形统计图如图所示.
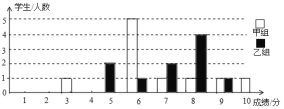
(1)补充完成下面的成绩统计分析表:
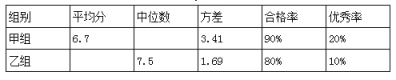
(2)小明同学说:“这次竞赛我得了7分,在我们小组中排名属中游偏上!”观察上表可知,小明是 组的学生;(填“甲”或“乙”)
(3)甲组同学说他们组的合格率、优秀率均高于乙组,所以他们组的成绩好于乙组.但乙组同学不同意甲组同学的说法,认为他们组的成绩要好于甲组,请你给出两条支持乙组同学观点的理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】梦想商店进了一批服装,进货单价为
 元,如果按每件
元,如果按每件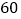 元出售,可销售
元出售,可销售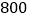 件,如果每件提价
件,如果每件提价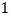 元出售,其销售量就减少
元出售,其销售量就减少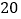 件.
件.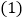 现在获利
现在获利 元,且销售成本不超过
元,且销售成本不超过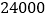 元,问这种服装销售单价应定多少元?这时应进多少服装?
元,问这种服装销售单价应定多少元?这时应进多少服装? 当销售单价应定多少元时,该商店获得最大利润?最大利润是多少元?
当销售单价应定多少元时,该商店获得最大利润?最大利润是多少元? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示的正方形网格中,
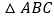 的顶点均在格点上,在所给直角坐标系中解答下列问题:
的顶点均在格点上,在所给直角坐标系中解答下列问题: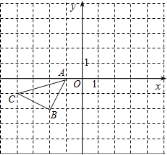
 分别写出点
分别写出点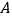 、
、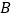 两点的坐标;
两点的坐标; 画出
画出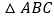 以
以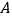 为旋转中心,将
为旋转中心,将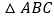 顺时针旋转
顺时针旋转 得到的
得到的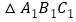 ;
;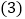 作出
作出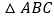 关于坐标原点成中心对称的
关于坐标原点成中心对称的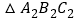 ;
;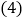 作出点
作出点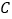 关于
关于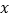 轴的对称点
轴的对称点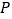 .若点
.若点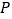 向右平移
向右平移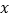 (
(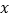 取整数)个单位长度后落在
取整数)个单位长度后落在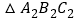 的内部,请直接写出
的内部,请直接写出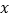 的值为________.
的值为________. -
科目: 来源: 题型:
查看答案和解析>>【题目】烟台享有“苹果之乡”的美誉.甲、乙两超市分别用3000元以相同的进价购进质量相同的苹果.甲超市销售方案是:将苹果按大小分类包装销售,其中大苹果400千克,以进价的2倍价格销售,剩下的小苹果以高于进价10%销售.乙超市的销售方案是:不将苹果按大小分类,直接包装销售,价格按甲超市大、小两种苹果售价的平均数定价.若两超市将苹果全部售完,其中甲超市获利2100元(其它成本不计).问:
(1)苹果进价为每千克多少元?
(2)乙超市获利多少元?并比较哪种销售方式更合算.
相关试题

