【题目】如图所示,抛物线![]() 的顶点为
的顶点为![]() ,与
,与![]() 轴交于
轴交于![]() 、
、![]() 两点,且
两点,且![]() ,与
,与![]() 轴交于点
轴交于点![]() .
.
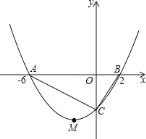
![]() 求抛物线的函数解析式;
求抛物线的函数解析式;
![]() 求
求![]() 的面积;
的面积;
![]() 能否在抛物线第三象限的图象上找到一点
能否在抛物线第三象限的图象上找到一点![]() ,使
,使![]() 的面积最大?若能,请求出点
的面积最大?若能,请求出点![]() 的坐标;若不能,请说明理由.
的坐标;若不能,请说明理由.
参考答案:
【答案】(1)![]() ;(2)
;(2)![]() ;(3)点
;(3)点![]() 的坐标是
的坐标是![]() .
.
【解析】
(1)根据顶点坐标公式即可求得a、b、c的值,即可解题;
(2)易求得点B、C的坐标,即可求得OC的长,即可求得![]() 的面积,即可解题;
的面积,即可解题;
(3)作PE⊥x轴于点E,交AC于点F,可将![]() 的面积转化为
的面积转化为![]() 和
和![]() 的面积之和,而这两个三角形有共同的底PF,这一个底上的高的和又恰好是A、C两点间的距离,因此若设设E(x,0),则可用x来表示
的面积之和,而这两个三角形有共同的底PF,这一个底上的高的和又恰好是A、C两点间的距离,因此若设设E(x,0),则可用x来表示![]() 的面积,得到关于x的一个二次函数,求得该二次函数最大值,即可解题.
的面积,得到关于x的一个二次函数,求得该二次函数最大值,即可解题.
![]() 设此函数的解析式为
设此函数的解析式为![]() ,
,
∵函数图象顶点为![]() ,
,
∴![]() ,
,
又∵函数图象经过点![]() ,
,
∴![]()
解得![]() ,
,
∴此函数的解析式为![]() ,即
,即![]() ;
;
![]() ∵点
∵点![]() 是函数
是函数![]() 的图象与
的图象与![]() 轴的交点,
轴的交点,
∴点![]() 的坐标是
的坐标是![]() ,
,
又当![]() 时,有
时,有![]() ,
,
解得![]() ,
,![]() ,
,
∴点![]() 的坐标是
的坐标是![]() ,
,
则![]() ;
;
![]() 假设存在这样的点,过点
假设存在这样的点,过点![]() 作
作![]() 轴于点
轴于点![]() ,交
,交![]() 于点
于点![]() .
.
设![]() ,则
,则![]() ,
,

设直线![]() 的解析式为
的解析式为![]() ,
,
∵直线![]() 过点
过点![]() ,
,![]() ,
,
∴![]() ,
,
解得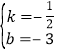 ,
,
∴直线![]() 的解析式为
的解析式为![]() ,
,
∴点![]() 的坐标为
的坐标为![]() ,
,
则![]() ,
,
∴![]()
![]()
![]() ,
,
∴当![]() 时,
时,![]() 有最大值
有最大值![]() ,
,
此时点![]() 的坐标是
的坐标是![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,小强在河的一边,要测河面的一只船B与对岸码头A的距离,他的做法如下:

①在岸边确定一点C,使C与A,B在同一直线上;
②在AC的垂直方向画线段CD,取其中点O;
③画DF⊥CD使F、O、A在同一直线上;
④在线段DF上找一点E,使E与O、B共线.
他说测出线段EF的长就是船B与码头A的距离.他这样做有道理吗?为什么?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知AP是△ABC的外角平分线,连结PB、PC.
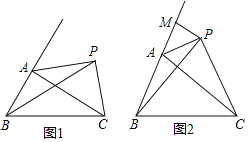
(1)如图1①若BP平分∠ABC,且∠ACB=28°,求∠APB的度数.
②若P与A不重合,请判断AB+AC与PB+PC的大小关系,并证明你的结论.
(2)如图2,若过点P作PM⊥BA,交BA的延长线于M点,且∠BPC=∠BAC,求:
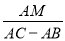 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数
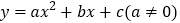 的图象如图所示,
的图象如图所示,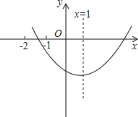
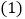 给出三个结论:①
给出三个结论:①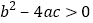 ;②
;② ;③
;③ ,其中正确结论的序号是:________.
,其中正确结论的序号是:________.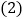 给出三个结论:①
给出三个结论:①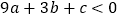 ;②
;②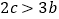 ;③
;③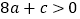 ,其中正确结论的序号是:________.
,其中正确结论的序号是:________. -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,直线AB交y轴于A(0,a),交x轴于B(b,0),且a,b满足(a﹣b)2+|3a+5b﹣88|=0.
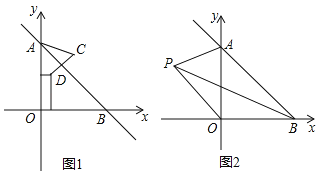
(1)求点A,B的坐标;
(2)如图1,已知点D(2,5),求点D关于直线AB对称的点C的坐标.
(3)如图2,若P是∠OBA的角平分线上的一点,∠APO=67.5°,求
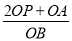 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在下列条件中,不能证明△ABD≌△ACD的是( ).

A.BD=DC, AB=AC B.∠ADB=∠ADC,BD=DC
C.∠B=∠C,∠BAD=∠CAD D. ∠B=∠C,BD=DC
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知a=2 002x+2 003,b=2 002x+2 004,c=2 002x+2 005,则多项式a2+b2+c2-ab-bc-ca的值为( )
A. 0 B. 1 C. 2 D. 3
相关试题

