【题目】如图,AD∥BC,连接BD,点E在BC上,点F在DC上,连接EF,且∠1=∠2.

(1)求证:EF∥BD;
(2)若BD平分∠ABC,∠A=130°,∠C=70°,求∠CFE的度数.
参考答案:
【答案】(1)证明见解析;(2)∠CFE=85°.
【解析】
(1)由AD∥BC知∠1=∠3,结合∠1=∠2得∠3=∠2,据此即可得证;
(2)由AD∥BC、∠A=130°知∠ABC=50°,再根据平分线定义及BD∥EF知∠3=∠2=25°,由三角形的内角和定理可得答案.
解:(1)如图,
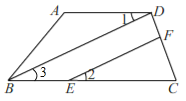
∵AD∥BC(已知),
∴∠1=∠3(两直线平行,内错角相等).
∵∠1=∠2,
∴∠3=∠2(等量代换).
∴EF∥BD(同位角相等,两直线平行).
(2)解:∵AD∥BC(已知),
∴∠ABC+∠A=180°(两直线平行,同旁内角互补).
∵∠A=130°(已知),
∴∠ABC=50°.
∵BD平分∠ABC(已知),
![]() ,
,
∴∠2=∠3=25°.
∵在△CFE中,∠CFE+∠2+∠C=180°(三角形内角和定理),∠C=70°,
∴∠CFE=85°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形ABCD中,对角线AC,BD相交于点O,AO=CO,BO=DO,且∠ABC+∠ADC=180°.

(1)求证:四边形ABCD是矩形;
(2)若∠ADF:∠FDC=3:2,DF⊥AC,求∠BDF的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】将长为20cm,宽为8cm的长方形白纸,按如图所示的方式粘合起来,粘合部分的宽为3cm.

(1)根据题意,将下面的表格补充完整.
白纸张数x(张)
1
2
3
4
5
…
纸条总长度y(cm)
20
54
71
…
(2)直接写出y与x的关系式.
(3)要使粘合后的长方形总面积为1656cm2,则需用多少张这样的白纸?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知矩形ABCD的两条对角线相交于点O,过点 A作AG⊥BD分别交BD、BC于点G、E.

(1)求证:BE2=EGEA;
(2)连接CG,若BE=CE,求证:∠ECG=∠EAC.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形ABCD的对角线AC、BD相交于点O,CE∥BD,DE∥AC,若AC=4,则四边形OCED的周长为( )
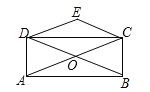
A.4B.8C.10D.12
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知∠1+∠2=180o, ∠3=∠B,试说明∠DEC+∠C=180o.请完成下列填空:

解:∵∠1+∠2=180o(已知)
又∵∠1+∠4=180o(平角定义)
∴∠2=∠4(________)
∴______∥______(_________)
∴∠3 = ∠ADE(__________)
又∵∠3=∠B(已知)
∴∠ADE=∠B(等量代换)
∴BC∥_____(_________)
∴∠DEC+∠C=180o(__________)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD为平行四边形,延长AD到E,使DE=AD,连接EB,EC,DB,下列条件中,不能使四边形DBCE成为菱形的是( )

A.AB=BEB.BE⊥DCC.∠ABE=90°D.BE平分∠DBC
相关试题

